题目内容
11.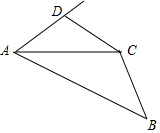 如图,AC平分∠DAB,∠ADC+∠B=180°,求证:CD=CB.
如图,AC平分∠DAB,∠ADC+∠B=180°,求证:CD=CB.
分析 作CF⊥AD交AD的延长线于F,作CE⊥AB于E,根据角平分线的性质得到CE=CF,证明△BEC≌△DFC,根据全等三角形的性质证明结论.
解答 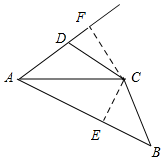 证明:作CF⊥AD,交AD的延长线于F,作CE⊥AB于E,
证明:作CF⊥AD,交AD的延长线于F,作CE⊥AB于E,
∵AC平分∠BAD,CE⊥AB,CF⊥AD,
∴CE=CF,
∵∠ADC+∠B=180°,又∠ADC+∠CDF=180°,
∴∠B=∠CDF,
在△BEC和△DFC中,
$\left\{\begin{array}{l}{∠B=∠CDF}\\{∠BEC=∠DFC}\\{CE=CF}\end{array}\right.$,
∴△BEC≌△DFC(AAS),
∴BC=CD.
点评 本题考查的是角平分线的性质和三角形全等的判定和性质,掌握角的平分线上的点到角的两边的距离相等、灵活运用三角形全等的判定定理和性质定理是解题的关键.

练习册系列答案
相关题目
19.H7N9时一种新型禽流感,其病毒颗粒呈多形性,其中球形病毒的最大直径为0.00000012米,这一直径用科学记数法表示为( )
| A. | 1.2×10-7米 | B. | 1.2×10-8米 | C. | 12×10-8米 | D. | 12×10-9米 |
16.已知点A(m2-2,5m+4)在第一象限角平分线上,则m的值为 ( )
| A. | 6 | B. | -1 | C. | 2或3 | D. | -1或6 |
3.数字3300用科学记数法表示为( )
| A. | 0.33×104 | B. | 3.3×103 | C. | 3.3×104 | D. | 33×103 |
 如图,矩形ABCD中,BC=2,将矩形ABCD绕点D顺时针旋转90°,点A,C分别落在点A′、C′处,并且点A′,C′,B在同一条直线上,则tan∠ABA′的值为$\frac{\sqrt{5}-1}{2}$.
如图,矩形ABCD中,BC=2,将矩形ABCD绕点D顺时针旋转90°,点A,C分别落在点A′、C′处,并且点A′,C′,B在同一条直线上,则tan∠ABA′的值为$\frac{\sqrt{5}-1}{2}$.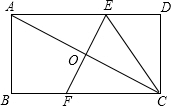 如图,将矩形纸片ABCD沿EF折叠,使点C与点A重合,连接CE,若AB=2,BC=3,则CE的长为$\frac{13}{6}$.
如图,将矩形纸片ABCD沿EF折叠,使点C与点A重合,连接CE,若AB=2,BC=3,则CE的长为$\frac{13}{6}$.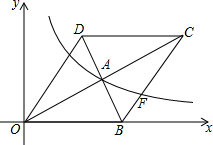 如图,在平面直角坐标系中,菱形OBCD的边OB在x轴上,反比例函数y=$\frac{k}{x}$(x>0)的图象经过菱形对角线的交点A,且与边BC交于点F,点A的坐标为(4,2).则点F的坐标是(6,$\frac{4}{3}$).
如图,在平面直角坐标系中,菱形OBCD的边OB在x轴上,反比例函数y=$\frac{k}{x}$(x>0)的图象经过菱形对角线的交点A,且与边BC交于点F,点A的坐标为(4,2).则点F的坐标是(6,$\frac{4}{3}$). 如图所示,等边三角形AEF内接于菱形ABCD,若AE=AB,求∠C的度数.
如图所示,等边三角形AEF内接于菱形ABCD,若AE=AB,求∠C的度数.