题目内容
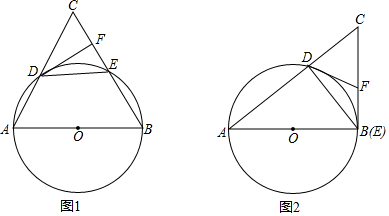
16. 如图,AB是⊙O的直径,点C在AB的延长线上,AD平分∠CAE交⊙O于点D,且AE⊥CD,垂足为点E.
如图,AB是⊙O的直径,点C在AB的延长线上,AD平分∠CAE交⊙O于点D,且AE⊥CD,垂足为点E.(1)求证:直线CE是⊙O的切线.
(2)若BC=3,CD=3$\sqrt{2}$,求弦AD的长.
分析 (1)连结OD,如图,由AD平分∠EAC得到∠1=∠3,加上∠1=∠2,则∠3=∠2,于是可判断OD∥AE,根据平行线的性质得OD⊥CE,然后根据切线的判定定理得到结论;
(2)由△CDB∽△CAD,可得$\frac{CD}{CA}$=$\frac{CB}{CD}$=$\frac{BD}{AD}$,推出CD2=CB•CA,可得(3$\sqrt{2}$)2=3CA,推出CA=6,推出AB=CA-BC=3,$\frac{BD}{AD}$=$\frac{3\sqrt{2}}{6}$=$\frac{\sqrt{2}}{2}$,设BD=$\sqrt{2}$K,AD=2K,在Rt△ADB中,可得2k2+4k2=5,求出k即可解决问题.
解答 (1)证明:连接OD,如图,
∵AD平分∠EAC,
∴∠1=∠3,
∵OA=OD,
∴∠1=∠2,
∴∠3=∠2,
∴OD∥AE,
∵AE⊥DC,
∴OD⊥CE,
∴CE是⊙O的切线;
(2)连接BD.
∵∠CDO=∠ADB=90°,
∴∠2=∠CDB=∠1,∵∠C=∠C,
∴△CDB∽△CAD,
∴$\frac{CD}{CA}$=$\frac{CB}{CD}$=$\frac{BD}{AD}$,
∴CD2=CB•CA,
∴(3$\sqrt{2}$)2=3CA,
∴CA=6,
∴AB=CA-BC=3,$\frac{BD}{AD}$=$\frac{3\sqrt{2}}{6}$=$\frac{\sqrt{2}}{2}$,设BD=$\sqrt{2}$K,AD=2K,
在Rt△ADB中,2k2+4k2=9,
∴k=$\frac{\sqrt{6}}{2}$,
∴AD=$\sqrt{6}$.
点评 本题考查切线的判定和性质、平行线的性质、切线的判定、勾股定理等知识,解题的关键是学会填空常用辅助线,灵活运用所学知识解决问题,属于中考常考题型.

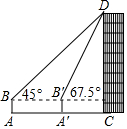 如图,数学实践活动小组要测量学校附近楼房CD的高度,在水平地面A处安置测倾器测得楼房CD顶部点D的仰角为45°,向前走20米到达A′处,测得点D的仰角为67.5°,已知测倾器AB的高度为1.6米,则楼房CD的高度约为(结果精确到0.1米,$\sqrt{2}$≈1.414)( )
如图,数学实践活动小组要测量学校附近楼房CD的高度,在水平地面A处安置测倾器测得楼房CD顶部点D的仰角为45°,向前走20米到达A′处,测得点D的仰角为67.5°,已知测倾器AB的高度为1.6米,则楼房CD的高度约为(结果精确到0.1米,$\sqrt{2}$≈1.414)( )| A. | 34.14米 | B. | 34.1米 | C. | 35.7米 | D. | 35.74米 |
| A. | y1>0>y2 | B. | y2>0>y1 | C. | y1>y2>0 | D. | y2>y1>0 |
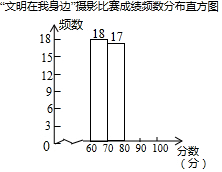 某校举行了“文明在我身边”摄影比赛.已知每幅参赛作品成绩记为x分(60≤x≤100).校方从600幅参赛作品中随机抽取了部分参赛作品,统计了它们的成绩,并绘制了如下不完整的统计图表.
某校举行了“文明在我身边”摄影比赛.已知每幅参赛作品成绩记为x分(60≤x≤100).校方从600幅参赛作品中随机抽取了部分参赛作品,统计了它们的成绩,并绘制了如下不完整的统计图表.“文明在我身边”摄影比赛成绩统计表
| 分数段 | 频数 | 频率 |
| 60≤x<70 | 18 | 0.36 |
| 70≤x<80 | 17 | c |
| 80≤x<90 | a | 0.24 |
| 90≤x≤100 | b | 0.06 |
| 合计 | 1 |
(1)统计表中c的值为0.34;样本成绩的中位数落在分数段70≤x<80中;
(2)补全频数分布直方图;
(3)若80分以上(含80分)的作品将被组织展评,试估计全校被展评作品数量是多少?
| A. | 2 | B. | 3 | C. | 5 | D. | 7 |
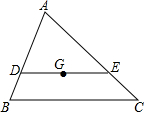 如图,G为△ABC的重心,DE过点G,且DE∥BC,交AB、AC,分别于D、E两点,则△ADE与△ABC的面积之比为$\frac{4}{9}$.
如图,G为△ABC的重心,DE过点G,且DE∥BC,交AB、AC,分别于D、E两点,则△ADE与△ABC的面积之比为$\frac{4}{9}$. 已知某几何体的三视图如图所示,其中俯视图为正六边形,则该几何体的表面积为48+12$\sqrt{3}$.
已知某几何体的三视图如图所示,其中俯视图为正六边形,则该几何体的表面积为48+12$\sqrt{3}$.