题目内容
6．
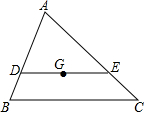如图，G为△ABC的重心，DE过点G，且DE∥BC，交AB、AC，分别于D、E两点，则△ADE与△ABC的面积之比为$\frac{4}{9}$．
分析 连接AG并延长交BC于H，根据重心的概念得到AG=2GH，根据平行线的性质、相似三角形的性质计算即可．
解答 解：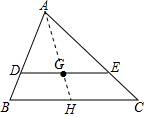
连接AG并延长交BC于H，
∵G为△ABC的重心，
∴AG=2GH，
∵DE∥BC，
∴$\frac{AD}{AB}$=$\frac{AG}{AH}$=$\frac{2}{3}$，
∵DE∥BC，
∴△ADE∽△ABC，相似比为$\frac{2}{3}$，
∴△ADE与△ABC的面积之比为$\frac{4}{9}$，
故答案为：$\frac{4}{9}$．
点评 本题考查的是三角形的重心的概念、相似三角形的判定和性质，三角形的重心是三角形三条中线的交点，且重心到顶点的距离是它到对边中点的距离的2倍．
练习册系列答案
期末冲刺100分创新金卷完全试卷系列答案
相关题目
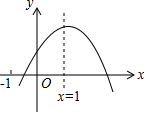已知二次函数y=ax2+bx+c的图象如图所示，给出下列结论：①abc＞0；②a-b+c＜0；③2a+b-c＜0；④4a+2b+c＞0，⑤若点（-$\frac{2}{3}$，y1）和（$\frac{7}{3}$，y2）在该图象上，则y1＞y2．其中正确的结论是②③④（填入正确结论的序号）
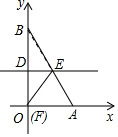将一个直角三角形纸片ABO，放置在平面直角坐标系中，点A（$\sqrt{3}$，0），点B（0，3），点O（0，0）
如图等边三角形ABC内接于圆，点P是圆上任意一点（P不与A、B、C重合），则∠APB=60°或120°．
如图，某校根据学生上学方式的一次抽样调查结果，绘制出一个未完成的扇形统计图，若该校共有学生1000人，则根据此估计步行上学的有400人．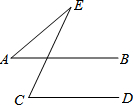
如图，已知AB∥CD，∠C=65°，∠E=25°，则∠A的度数为40°．
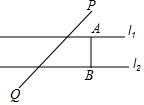如图，已知直线l1∥l2，l1、l2之间的距离为8，点P到直线l1的距离为6，点Q到直线l2的距离为4，PQ=4$\sqrt{30}$，在直线l1上有一动点A，直线l2上有一动点B，满足AB⊥l2，且PA+AB+BQ最小，此时PA+BQ=16．
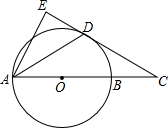如图，AB是⊙O的直径，点C在AB的延长线上，AD平分∠CAE交⊙O于点D，且AE⊥CD，垂足为点E．