题目内容
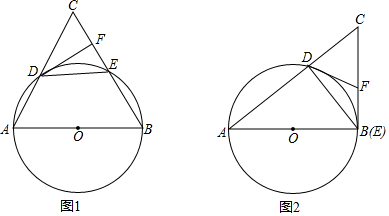
5.已知:AB为⊙O的直径,AB=2,弦DE=1,直线AD与BE相交于点C,弦DE在⊙O上运动且保持长度不变,⊙O的切线DF交BC于点F.(1)如图1,若DE∥AB,求证:CF=EF;
(2)如图2,当点E运动至与点B重合时,试判断CF与BF是否相等,并说明理由.
分析 (1)如图1,连接OD、OE,证得△OAD、△ODE、△OEB、△CDE是等边三角形,进一步证得DF⊥CE即可证得结论;
(2)根据切线的性质以及等腰三角形的性质即可证得结论.
解答 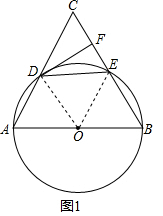 证明:如图1,连接OD、OE,
证明:如图1,连接OD、OE,
∵AB=2,
∴OA=OD=OE=OB=1,
∵DE=1,
∴OD=OE=DE,
∴△ODE是等边三角形,
∴∠ODE=∠OED=60°,
∵DE∥AB,
∴∠AOD=∠ODE=60°,∠EOB=∠OED=60°,
∴△AOD和△BOE是等边三角形,
∴∠OAD=∠OBE=60°,
∴∠CDE=∠OAD=60°,∠CED=∠OBE=60°,
∴△CDE是等边三角形,
∵DF是⊙O的切线,
∴OD⊥DF,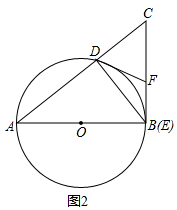
∴∠EDF=90°-60°=30°,
∴∠DFE=90°,
∴DF⊥CE,
∴CF=EF;
(2)相等;
如图2,点E运动至与点B重合时,BC是⊙O的切线,
∵⊙O的切线DF交BC于点F,
∴BF=DF,
∴∠BDF=∠DBF,
∵AB是直径,
∴∠ADB=∠BDC=90°,
∴∠FDC=∠C,
∴DF=CF,
∴BF=CF.
点评 本题考查了切线的性质、平行线的性质、等边三角形的判定、等腰三角形的判定和性质,作出辅助线构建等边三角形是解题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
13.某校排球队10名队员的身高(厘米)如下:
195,186,182,188,188,182,186,188,186,188.
这组数据的众数和中位数分别是( )
195,186,182,188,188,182,186,188,186,188.
这组数据的众数和中位数分别是( )
| A. | 186,188 | B. | 188,187 | C. | 187,188 | D. | 188,186 |
10.5的相反数是( )
| A. | 5 | B. | -5 | C. | $\frac{1}{5}$ | D. | -$\frac{1}{5}$ |
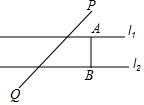 如图,已知直线l1∥l2,l1、l2之间的距离为8,点P到直线l1的距离为6,点Q到直线l2的距离为4,PQ=4$\sqrt{30}$,在直线l1上有一动点A,直线l2上有一动点B,满足AB⊥l2,且PA+AB+BQ最小,此时PA+BQ=16.
如图,已知直线l1∥l2,l1、l2之间的距离为8,点P到直线l1的距离为6,点Q到直线l2的距离为4,PQ=4$\sqrt{30}$,在直线l1上有一动点A,直线l2上有一动点B,满足AB⊥l2,且PA+AB+BQ最小,此时PA+BQ=16.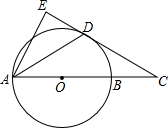 如图,AB是⊙O的直径,点C在AB的延长线上,AD平分∠CAE交⊙O于点D,且AE⊥CD,垂足为点E.
如图,AB是⊙O的直径,点C在AB的延长线上,AD平分∠CAE交⊙O于点D,且AE⊥CD,垂足为点E. 如图,直线l1∥l2,∠1=20°,则∠2+∠3=200°.
如图,直线l1∥l2,∠1=20°,则∠2+∠3=200°. 如图,已知直线a∥b,∠1=70°,则∠2=110°.
如图,已知直线a∥b,∠1=70°,则∠2=110°.