题目内容
10.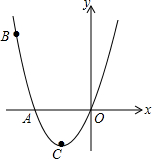 如图,已知抛物线经过点A(-2,0),B(-3,3)及原点O,顶点为C.
如图,已知抛物线经过点A(-2,0),B(-3,3)及原点O,顶点为C.(1)求抛物线的函数解析式;
(2)连接BC交x轴于点F.试在y轴负半轴上找一点P,使得△POC∽△BOF.
分析 (1)抛物线的解析式为y=ax2+bx+c (a≠0),把A、B、C的坐标代入求出即可;
(2)求出∠BOF=∠POC,求出OB、OF、OC的长,根据相似得出比例式,代入求出即可.
解答 解:(1)设抛物线的解析式为y=ax2+bx+c (a≠0),
将点A(-2,0)、B(-3,3)、0(0,0),
代入可得:$\left\{\begin{array}{l}{4a-2b+c=0}\\{9a-3b+c=3}\\{c=0}\end{array}\right.$
解得:a=1,b=2,c=0,
所以抛物线的解析式为y=x2+2x;
(2)如图,∵y=x2+2x=(x+1)2-1,
∴顶点C的坐标为(-1,-1).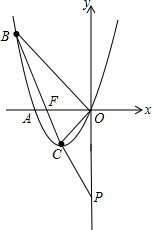
∵B(-3,3),
∴tan∠BOF=$\frac{3}{3}$=1,tan∠POC=$\frac{1}{1}$=1,
∴∠BOF=45°,∠POC=45°.
∴∠POC=∠BOF,
∴∠POC=45°=∠BOF,
设直线BC的解析式为y=kx+b(k≠0),
∵直线经过点B(-3,3)、C(-1,-1),
∴$\left\{\begin{array}{l}{-3k+b=3}\\{-k+b=-1}\end{array}\right.$
解得:k=-2,b=-3,
∴直线BC解析式为y=-2x-3,
令y=0,得x=-$\frac{3}{2}$,
因此,点F(-$\frac{3}{2}$,0),
∴OF=$\frac{3}{2}$,OB=$\sqrt{{3}^{2}+{3}^{2}}$=3$\sqrt{2}$,
OC=$\sqrt{{1}^{2}+{1}^{2}}$=$\sqrt{2}$,
∵∠POC=∠BOF,
∴当$\frac{OP}{OB}$=$\frac{OC}{OF}$时,△POC∽△BOF,
代入求出OP=4,
即当P点的坐标为(0,-4)时,△POC∽△BOF.
点评 本题考查了用待定系数法求二次函数、一次函数的解析式,相似三角形的性质和判定的应用,能求出符合的所有情况是解此题的关键.

 阅读快车系列答案
阅读快车系列答案| A. | 30° | B. | 20° | C. | 70° | D. | 110° |
| A. | $\frac{1}{5}(x+y)$ | B. | $\frac{a}{3}$ | C. | $\frac{ab}{2}+\frac{1}{c}$ | D. | $\frac{x}{2}+y$ |
| A. | (-m-n)(-m+n) | B. | $(\frac{1}{2}x+1)(-\frac{1}{2}x-1)$ | C. | (3x-y)(-3x+y) | D. | (2a+b)(2b-a) |
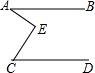 如图,已知直线AB∥CD,∠A=20°,∠C=40°,则∠E=( )
如图,已知直线AB∥CD,∠A=20°,∠C=40°,则∠E=( )| A. | 20° | B. | 40° | C. | 60° | D. | 80° |
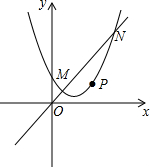 如图,抛物线y=ax2+bx+c(a≠0)与直线y=kx(k≠0)相交于点M(1,1),N(3,3),且这条抛物线的对称轴为x=1.
如图,抛物线y=ax2+bx+c(a≠0)与直线y=kx(k≠0)相交于点M(1,1),N(3,3),且这条抛物线的对称轴为x=1.