题目内容
17.在平面直角坐标系中,已知一次函数y=2x+1的图象经过P1(x1,y1),P2(x2,y2)两点,若x1<x2,则y1与y2的大小关系为( )| A. | y1>y2 | B. | y1=y2 | ||
| C. | y1<y2 | D. | y1与y2的大小关系不能确定 |
分析 一次函数图象上点的坐标特征,把P1(x1,y1),P2(x2,y2)代入解析式可得到y1=2x1+1,y2=2x2+1,然后利用x1<x2比较y1与y2的大小.
解答 解:∵一次函数y=2x+1的图象经过P1(x1,y1),P2(x2,y2)两点,
∴y1=2x1+1,y2=2x2+1,
而x1<x2,
∴y1<y2.
故选C.
点评 本题考查了一次函数图象上点的坐标特征:一次函数y=kx+b,(k≠0,且k,b为常数)的图象是一条直线.它与x轴的交点坐标是(-$\frac{b}{k}$,0);与y轴的交点坐标是(0,b).直线上任意一点的坐标都满足函数关系式y=kx+b.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
12.下列四组数中,能作为直角三角形三边长的是( )
| A. | 8,15,17 | B. | 4,5,6 | C. | 2,3,4 | D. | 1,$\sqrt{2},3$ |
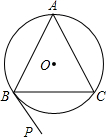 如图,△ABC内接于⊙O,已知⊙O的半径R=1,BP为⊙O切线,BC=$\sqrt{3}$,则∠CBP的度数为60°.
如图,△ABC内接于⊙O,已知⊙O的半径R=1,BP为⊙O切线,BC=$\sqrt{3}$,则∠CBP的度数为60°.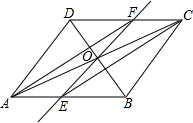 如图,在平行四边形ABCD中,对角线AC与BD交于点O,经过点O的直线交AB于E,交CD于F,连接AF,CE,求证:四边形AFCE是平行四边形.
如图,在平行四边形ABCD中,对角线AC与BD交于点O,经过点O的直线交AB于E,交CD于F,连接AF,CE,求证:四边形AFCE是平行四边形.