题目内容
9.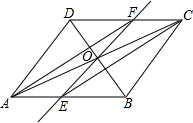 如图,在平行四边形ABCD中,对角线AC与BD交于点O,经过点O的直线交AB于E,交CD于F,连接AF,CE,求证:四边形AFCE是平行四边形.
如图,在平行四边形ABCD中,对角线AC与BD交于点O,经过点O的直线交AB于E,交CD于F,连接AF,CE,求证:四边形AFCE是平行四边形.
分析 由平行四边形的性质得出OA=OC,AB∥CD,得出∠OAE=∠OCF,由ASA证明△AOE≌△COF,得出对应边相等OE=OF,即可得出结论.
解答 证明:∵四边形ABCD是平行四边形,
∴OA=OC,AB∥CD,
∴∠OAE=∠OCF,
在△AOE和△COF中,$\left\{\begin{array}{l}{∠OAE=∠OCF}&{\;}\\{OA=OC}&{\;}\\{∠AOE=∠COF}&{\;}\end{array}\right.$,
∴△AOE≌△COF(ASA),
∴OE=OF,
又∵OA=OC,
∴四边形AFCE是平行四边形.
点评 本题考查了平行四边形的判定与性质、全等三角形的判定与性质;熟练掌握平行四边形的性质,并能进行推理论证是解决问题的关键.

练习册系列答案
相关题目
19. 如图,C是⊙O上一点,O是圆心,若∠C=35°,则∠AOB的度数为( )
如图,C是⊙O上一点,O是圆心,若∠C=35°,则∠AOB的度数为( )
 如图,C是⊙O上一点,O是圆心,若∠C=35°,则∠AOB的度数为( )
如图,C是⊙O上一点,O是圆心,若∠C=35°,则∠AOB的度数为( )| A. | 35° | B. | 55° | C. | 70° | D. | 105° |
17.在平面直角坐标系中,已知一次函数y=2x+1的图象经过P1(x1,y1),P2(x2,y2)两点,若x1<x2,则y1与y2的大小关系为( )
| A. | y1>y2 | B. | y1=y2 | ||
| C. | y1<y2 | D. | y1与y2的大小关系不能确定 |
18.在10分钟的时间内,分针转过的角度是( )
| A. | 15° | B. | 30° | C. | 15° | D. | 60° |
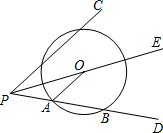 如图,射线PE平分∠CPD,O为射线PE上一点,以O为圆心作⊙O,与PD边交于点A、点B,连结OA,且OA∥PC.
如图,射线PE平分∠CPD,O为射线PE上一点,以O为圆心作⊙O,与PD边交于点A、点B,连结OA,且OA∥PC. 一个长方形门框内框的尺寸(单位:分米)如图所示,一块长4米,宽3米的玻璃板(厚度不计),能否从门框内通过?为什么?
一个长方形门框内框的尺寸(单位:分米)如图所示,一块长4米,宽3米的玻璃板(厚度不计),能否从门框内通过?为什么? 如图的几何体,是由一个圆柱体从正中央挖去了一个与它等高的长方体后形成的,其俯视图如下,这个几何体的主视图是( )
如图的几何体,是由一个圆柱体从正中央挖去了一个与它等高的长方体后形成的,其俯视图如下,这个几何体的主视图是( )



 如图所示,△ABC中,CD⊥AB于D,且AC>BC.
如图所示,△ABC中,CD⊥AB于D,且AC>BC.