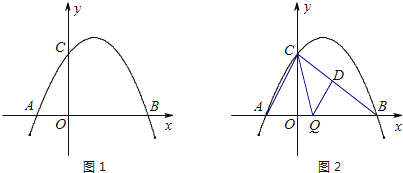题目内容
如图,已知直线a∥b∥c,且a与b之间的距离为3,且b与c之间的距离为1,点A到直线a的距离为2,点B到直线c的距离为3,AB=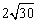 .试在直线a上找一点M,在直线c上找一点N,满足MN⊥a且AM+MN+NB的长度和最短,则此时AM+NB=【 】
.试在直线a上找一点M,在直线c上找一点N,满足MN⊥a且AM+MN+NB的长度和最短,则此时AM+NB=【 】

A.12 B.10 C.8 D.6
C。
【考点】轴对称的应用(最短线路问题),平行线之间的 距离,平行四边形的判定和性质,勾股定理。
距离,平行四边形的判定和性质,勾股定理。
【分析】MN表示直线a与直线c之间的距离,是定值,只要满足AM+NB的值最小即可,如图,作点A关于直线a的对称点A′,连接A′B交直线c与点N,过点N作NM⊥直线a,连接AM,




练习册系列答案
相关题目
 与运行的水平距离x(m)满足关系式
与运行的水平距离x(m)满足关系式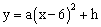 。已知球网与O点
。已知球网与O点 的水平距离为9m,高度为2.43m,球场的边界距O点的水平距离为18m。
的水平距离为9m,高度为2.43m,球场的边界距O点的水平距离为18m。 二次函数中二次项系数a的最大值。
二次函数中二次项系数a的最大值。


 中点O为圆心、OA长为半径作⊙O,⊙O经过B、D两点,过点B作BK⊥AC,垂足为K,过点D作
中点O为圆心、OA长为半径作⊙O,⊙O经过B、D两点,过点B作BK⊥AC,垂足为K,过点D作 DH∥KB,DH分别与AC、AB、⊙O及CB的延长线相交于点E、F、G、H。
DH∥KB,DH分别与AC、AB、⊙O及CB的延长线相交于点E、F、G、H。

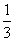
 a(a为常数),求BK的长(用含a的代数式表示)。
a(a为常数),求BK的长(用含a的代数式表示)。
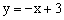 沿y轴方向平移m个单位后,与直线
沿y轴方向平移m个单位后,与直线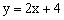 的交点在第二象限,则m的取值范围是【 】
的交点在第二象限,则m的取值范围是【 】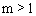 B.
B.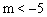 C.
C.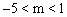 D.
D.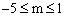

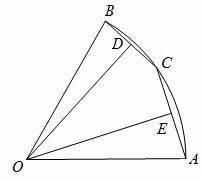
 )如图2,连接AC、BC,点Q是线段0B上一个动点(点Q不与点0、B重合).过点Q作QD∥AC交BC于点D,设Q点坐标(m,0),当△CDQ面积S最大时,求m的值.
)如图2,连接AC、BC,点Q是线段0B上一个动点(点Q不与点0、B重合).过点Q作QD∥AC交BC于点D,设Q点坐标(m,0),当△CDQ面积S最大时,求m的值.