题目内容
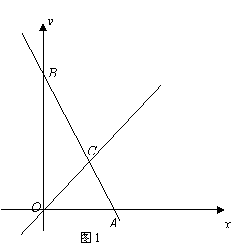
如图(1),Rt△ABC和Rt△EFD中,AC与DE重合,AB=EF=1,∠BAC=∠DEF=90º,∠ ACB=∠EDF=30º,固定△ABC,将△DEF绕点A顺时针旋转,当DF边与AB边重合时,旋转中止。现不考虑旋转开始和结束 时重合的情况,设DE,DF(或它们的延长线)分别交BC(或它的延长线) 于G,H点,如图(2)
时重合的情况,设DE,DF(或它们的延长线)分别交BC(或它的延长线) 于G,H点,如图(2)
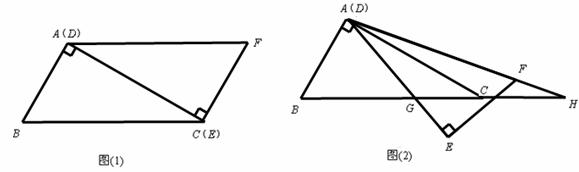
(1)问:始终与△AGC相似的三角形是 ;
(2)设CG=x,BG=y,求y关于x的函数关系式;
(3)问:当x为何值时,△HGA是等腰三角形。
(1)△HGA。
(2)∵∠BAC =90º,∠ ACB =30º,AB =1,∴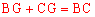 ,即
,即 。∴
。∴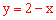 。
。
又∵BC=2,∴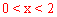 。
。
∴y关于x的函数关系式为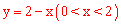 。
。
(3)由(1)知,△AGC∽△HGA,若△HGA是等腰三角形,则AGC也是等腰三角形。所以分两种情况:
①当CG=AG时,AG是Rt△ABC斜边上的中线, 此时,x=CG=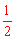 BC=1。
BC=1。
②当CG= CA时, x=CG= 。
。
∴当x=1或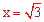 时,△AGH是等腰三角形。
时,△AGH是等腰三角形。
【考点】面动旋转问题,含30度角直角三角形的性质,三角形内角和外角性质,相似三角形的判定和性质,等腰三角形的判定,由实际问题列函数关系式,分类思想的应用。

(3)考虑CG=AG和CG= CA两种情况分别求解即可。

练习册系列答案
相关题目



 轴交于点A
轴交于点A ,与
,与 轴交于点B,与直线OC:
轴交于点B,与直线OC: 交于点C.
交于点C.

 ,
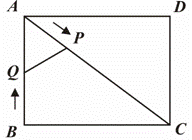
, 的平分线ON,若AB⊥ON,垂足为E, OA=4
的平分线ON,若AB⊥ON,垂足为E, OA=4 ,P、Q分别为线段OA、OE上的动点,连结AQ与PQ,试探索AQ+PQ是否存在最小值?若存在,求出这个最小值;若不存在,说明理由.
,P、Q分别为线段OA、OE上的动点,连结AQ与PQ,试探索AQ+PQ是否存在最小值?若存在,求出这个最小值;若不存在,说明理由.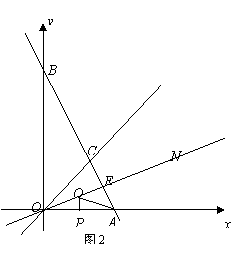



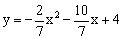 ,与x轴的另一交点为E,连结CE。
,与x轴的另一交点为E,连结CE。 的坐标;
的坐标;
 )如图2,连接AC、BC,点Q是线段0B上一个动点(点Q不与点0、B重合).过点Q作QD∥AC交BC于点D,设Q点坐标(m,0),当△CDQ面积S最大时,求m的值.
)如图2,连接AC、BC,点Q是线段0B上一个动点(点Q不与点0、B重合).过点Q作QD∥AC交BC于点D,设Q点坐标(m,0),当△CDQ面积S最大时,求m的值.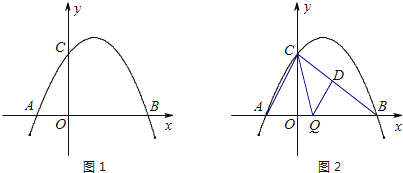
 ,2)。将△
,2)。将△ ABC沿x轴的反方向平移,在第二象限内B、C两点的对应点B′、C′正好落在反比例函数
ABC沿x轴的反方向平移,在第二象限内B、C两点的对应点B′、C′正好落在反比例函数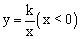 的图像上,直线B′C′交y轴于点G。问是否存在x轴上的点M和
的图像上,直线B′C′交y轴于点G。问是否存在x轴上的点M和 反比例函数图像上的点P,使得四边形PGMC′是平行四边形。如果存
反比例函数图像上的点P,使得四边形PGMC′是平行四边形。如果存 在,请
在,请 求出点M和点P的坐标;如果不存在,请说明理由。
求出点M和点P的坐标;如果不存在,请说明理由。