题目内容
14.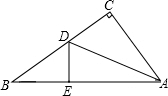 如图,有一个直角三角形纸片,两直角边AC=6cm,BC=8cm,AD平分∠CAB,DE⊥AB于点E,则CD=3cm.
如图,有一个直角三角形纸片,两直角边AC=6cm,BC=8cm,AD平分∠CAB,DE⊥AB于点E,则CD=3cm.
分析 先利用勾股定理求出AB,根据角平分线的性质得到DC=DE,然后得出△ADC≌△ADE,求出AE=AC与BE的长,设CD=x,则DE=x,DB=8-x,在Rt△BDE中,利用勾股定理得到BD2=DE2+BE2,即(8-x)2=x2+42,再解方程即可得到CD的长.
解答 解:∵在Rt△ABC中,AC=6cm,BC=8cm,
∴AB=10cm,
∵AD平分∠CAB,DE⊥AB,
∴DC=DE,
在Rt△ADC和Rt△ADE中,
∵$\left\{\begin{array}{l}{AD=AD}\\{DC=DE}\end{array}\right.$,
∴Rt△ADC≌Rt△ADE,
∴AE=AC=6cm,
∴BE=AB-AE=10-6=4cm,
设CD=x,则DE=x,DB=8-x,
在Rt△BDE中,BD2=DE2+BE2,即(8-x)2=x2+42,
解得x=3,
则CD的长为3cm.
故答案为:3cm.
点评 本题考查了角平分线的性质:角平分线上的点到角的两边的距离相等.也考查了勾股定理以及三角形全等的判定与性质.

练习册系列答案
 寒假乐园北京教育出版社系列答案
寒假乐园北京教育出版社系列答案
相关题目
4.下列是一元二次方程的是( )
| A. | x2+4x+5 | B. | -3x2+4x=5 | C. | x2+4y=5 | D. | x2+$\frac{1}{x}$=5 |
6.下列方程是一元二次方程的是( )
| A. | 2x2-7=3y+1 | B. | 5x2+$\frac{1}{x}$+4=0 | C. | $\frac{\sqrt{7}}{3}$x-$\sqrt{5}$=$\frac{{x}^{2}}{2}$+x | D. | ax2+bx+c=0 |
 有理数a、b在数轴上对应点的位置如图所示,化简|a+b|+|a|+|-b|-|1-b|=b+1.
有理数a、b在数轴上对应点的位置如图所示,化简|a+b|+|a|+|-b|-|1-b|=b+1.