题目内容
6.当m分别取何值时关于x的方程(m-1)x2+(2m-1)x+m-1=0:(1)有两个不相等的实数根;
(2)有两个相等的实数根;
(3)有两个实数根;
(4)有一个实数根;
(5)有实数根.
分析 (1)当方程有两个不相等实数根时,△>0,且m-1≠0;
(2)当方程有两个相等实数根时,△=0,且m-1≠0;
(3)当方程有两个实数根时,△=≥0,且m-1≠0;
(4)当方程有一个实数根时,方程是一元一次方程,故m-1=0;
(5)当方程有实数根时,该方程可能是一元二次方程或者一元一次方程,可得△≥0或m-1=0.
解答 解:关于x的方程(m-1)x2+(2m-1)x+m-1=0中,
△=(2m-1)2-4(m-1)(m-1)=4m-3,
(1)当方程有两个不相等实数根时,△=4m-3>0,且m-1≠0,
解得:m>$\frac{3}{4}$,且m≠1;
(2)当方程有两个相等实数根时,△=4m-3=0,且m-1≠0,
解得:m=$\frac{3}{4}$;
(3)当方程有两个实数根时,△=4m-3≥0,且m-1≠0,
解得:m≥$\frac{3}{4}$,且m≠1;
(4)当方程有一个实数根时,m-1=0,即m=1;
(5)当方程有实数根时,△=4m-3≥0或m-1=0,
解得:m≥$\frac{3}{4}$或m=1.
点评 此题考查一元二次方程根的情况与判别式△的关系:(1)△>0?方程有两个不相等的实数根;(2)△=0?方程有两个相等的实数根;(3)△<0?方程没有实数根,同时还应该注意判断该方程有无可能不是一元二次方程.

练习册系列答案
相关题目
11.方程(x-1)(x+2)=-2的根为( )
| A. | x1=1,x2=-2 | B. | x1=0,x2=1 | C. | x1=0,x2=-1 | D. | x1=1,x2=-1 |
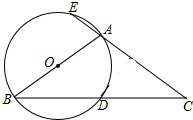 如图,△ABC中,AB=AC,以AB为直径的⊙O与BC相交于点D,与CA的延长线相交于点E,若AC=3AE,则tan∠ABC=$\frac{\sqrt{2}}{2}$.
如图,△ABC中,AB=AC,以AB为直径的⊙O与BC相交于点D,与CA的延长线相交于点E,若AC=3AE,则tan∠ABC=$\frac{\sqrt{2}}{2}$.