题目内容
2.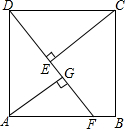 如图,正方形ABCD中,F为AB边上一点,过点A,C分别作DF的垂线,垂足为G和E,若AG=3,EG=1,则BF的长为$\frac{5}{4}$.
如图,正方形ABCD中,F为AB边上一点,过点A,C分别作DF的垂线,垂足为G和E,若AG=3,EG=1,则BF的长为$\frac{5}{4}$.
分析 利用正方形的性质结合全等三角形的判定与性质得出DG的长进而求出AD,再利用相似三角形的判定与性质得出答案.
解答  解:∵四边形ABCD是正方形,
解:∵四边形ABCD是正方形,
∴∠ADG+∠CDE=90°,
∵∠CDE+∠DCE=90°,
∴∠ADG=∠DCE,
在△DEC和△AGD中,
$\left\{\begin{array}{l}{∠AGD=∠DEC}\\{∠GDA=∠ECD}\\{AD=DC}\end{array}\right.$,
∴△DEC≌△AGD(AAS),
∴AG=DE=3,
∵EG=1,
∴DG=4,
∴AD=5,
∵∠ADF=∠GDA,∠AGD=∠DAF,
∴△ADG∽△FDA,
∴$\frac{AG}{AF}$=$\frac{DG}{AD}$,
即$\frac{3}{AF}$=$\frac{4}{5}$,
解得:AF=$\frac{15}{4}$,
∴BF=5-AF=5-$\frac{15}{4}$=$\frac{5}{4}$.
故答案为:$\frac{5}{4}$.
点评 此题主要考查了全等三角形的判定与性质以及相似三角形的判定与性质和正方形的性质,得出AD的长是解题关键.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
12.八边形的外角和为( )
| A. | 180° | B. | 360° | C. | 900° | D. | 1260° |
11.方程(x-1)(x+2)=-2的根为( )
| A. | x1=1,x2=-2 | B. | x1=0,x2=1 | C. | x1=0,x2=-1 | D. | x1=1,x2=-1 |
 如图,已知一次函数y=x-2与反比例函数$y=\frac{3}{x}$的图象交于A、B两点.
如图,已知一次函数y=x-2与反比例函数$y=\frac{3}{x}$的图象交于A、B两点. 如图,直线y=-x+2与x轴相交于点A,与y轴相交于点B.直线y=-2x+b经过点A,与y轴相交丁点C,在直线AC上是否存在点D,使∠BDA=45°?若存在,求点D的坐标;若不存在.说明理由.
如图,直线y=-x+2与x轴相交于点A,与y轴相交于点B.直线y=-2x+b经过点A,与y轴相交丁点C,在直线AC上是否存在点D,使∠BDA=45°?若存在,求点D的坐标;若不存在.说明理由. 已知AD⊥BC,CE⊥AB,AB=BC.
已知AD⊥BC,CE⊥AB,AB=BC.