题目内容
6.先化简再求值:($\frac{x}{x+1}$-$\frac{1}{{x}^{2}+x}$)÷(x-1),其中x=$\sqrt{3}$.分析 原式括号中两项通分并利用同分母分式的减法法则计算,同时利用除法法则变形,约分得到最简结果,把x的值代入计算即可求出值.
解答 解:原式=$\frac{{x}^{2}-1}{x(x+1)}$•$\frac{1}{x-1}$=$\frac{(x+1)(x-1)}{x(x+1)}$•$\frac{1}{x-1}$=$\frac{1}{x}$,
当x=$\sqrt{3}$,原式=$\frac{\sqrt{3}}{3}$.
点评 此题考查了分式的化简求值,熟练掌握运算法则是解本题的关键.

练习册系列答案
相关题目
16.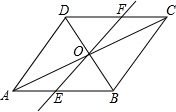 如图,在平行四边形ABCD中,对角线AC,BD并于点O,经过点O的直线交AB于E,交CD于F.
如图,在平行四边形ABCD中,对角线AC,BD并于点O,经过点O的直线交AB于E,交CD于F.
①求证:OE=OF.
②连接DE,BF,则EF与BD满足什么条件时,四边形DEBF是矩形?请说明理由.
 如图,在平行四边形ABCD中,对角线AC,BD并于点O,经过点O的直线交AB于E,交CD于F.
如图,在平行四边形ABCD中,对角线AC,BD并于点O,经过点O的直线交AB于E,交CD于F.①求证:OE=OF.
②连接DE,BF,则EF与BD满足什么条件时,四边形DEBF是矩形?请说明理由.
1.把$\sqrt{\frac{8}{9}}$化为最简二次根式是( )
| A. | $\frac{\sqrt{8}}{3}$ | B. | $\frac{{2\sqrt{2}}}{{\sqrt{9}}}$ | C. | $\frac{2}{3}$ | D. | $\frac{2\sqrt{2}}{3}$ |
18.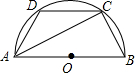 如图,AB是半圆O的直径,D是$\widehat{AC}$上一点,若∠BAC=35°,则∠ADC的度数是( )
如图,AB是半圆O的直径,D是$\widehat{AC}$上一点,若∠BAC=35°,则∠ADC的度数是( )
 如图,AB是半圆O的直径,D是$\widehat{AC}$上一点,若∠BAC=35°,则∠ADC的度数是( )
如图,AB是半圆O的直径,D是$\widehat{AC}$上一点,若∠BAC=35°,则∠ADC的度数是( )| A. | 100° | B. | 120° | C. | 125° | D. | 130° |
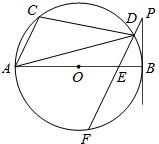 如图,已知AB是⊙O的直径,点C、D在⊙O上,过D点作PF∥AC交⊙O于F,交AB于点E,∠BPF=∠ADC.
如图,已知AB是⊙O的直径,点C、D在⊙O上,过D点作PF∥AC交⊙O于F,交AB于点E,∠BPF=∠ADC. 如图,在平面直角坐标系xOy中,一次函数y=-x+b的图象与反比例函数y=-$\frac{1}{x}$(x<0)交于点A,与x轴交于点B,则OA2-OB2的值为( )
如图,在平面直角坐标系xOy中,一次函数y=-x+b的图象与反比例函数y=-$\frac{1}{x}$(x<0)交于点A,与x轴交于点B,则OA2-OB2的值为( )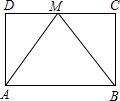 如图,在?ABCD中,点M为CD边的中点,△ABM是等边三角形.求证:?ABCD是矩形.
如图,在?ABCD中,点M为CD边的中点,△ABM是等边三角形.求证:?ABCD是矩形.