题目内容
16.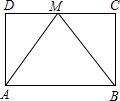 如图,在?ABCD中,点M为CD边的中点,△ABM是等边三角形.求证:?ABCD是矩形.
如图,在?ABCD中,点M为CD边的中点,△ABM是等边三角形.求证:?ABCD是矩形.
分析 欲证明平行四边形ABCD是矩形,只需证得该四边形的一个内角是90度即可.
解答 证明:∵△BCM是等边三角形,
∴CM=BM,∠MBC=∠MCB=∠BMC=60°,
又∵四边形ABCD是平行四边形,
∴AD∥BC,
∴∠AMB=∠MBC=60°,∠DMC=∠DCM=60°.
则∠AMB=∠DMC,∠MBC=∠DCM,
∵M是AD的中点,
∴AM=DM.
∴在△AMB与△DMC中,
$\left\{\begin{array}{l}{∠ABM=∠DCM}\\{∠AMB=∠DMC}\\{AM=DM}\end{array}\right.$,
∴△AMB≌△DMC(AAS),
∴∠A=∠D.
又∠A+∠D=180°,
∴∠A=∠D=90°,
∴平行四边形ABCD是矩形.
点评 本题考查了矩形的判定.此题根据矩形的定义进行证明的:有一个角是直角的平行四边形是矩形.

练习册系列答案
 名校通行证有效作业系列答案
名校通行证有效作业系列答案
相关题目
5.若y-1与2-x成正比例,则下列说法正确的是( )
| A. | y是x的一次函数 | B. | y是x的正比例函数 | ||
| C. | y是x的函数但不是正比例函数 | D. | y不是x的函数 |
 如图,点A,B,C在⊙O上,若∠ACO=24°,AB∥OC,则∠BOC的度数是48°.
如图,点A,B,C在⊙O上,若∠ACO=24°,AB∥OC,则∠BOC的度数是48°.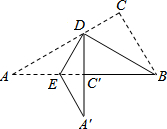 如图,在Rt△ABC中,∠ACB=90°,将△ABC沿BD折叠,点C恰巧落在边AB上的C′处,折痕为BD,再将其沿DE折叠,使点A落在DC′的延长线上的A′处.若△BED与△ABC相似,则相似比$\frac{BD}{AC}$=$\frac{2}{3}$.
如图,在Rt△ABC中,∠ACB=90°,将△ABC沿BD折叠,点C恰巧落在边AB上的C′处,折痕为BD,再将其沿DE折叠,使点A落在DC′的延长线上的A′处.若△BED与△ABC相似,则相似比$\frac{BD}{AC}$=$\frac{2}{3}$.
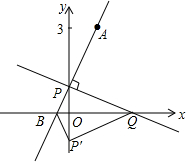 如图,在平面直角坐标系中,O是坐标原点,点A的坐标是(1,3),点P的坐标是(0,b)(b≠0).直线AP交x轴于点B,记点P关于x轴的对称点为P′,点Q为x轴上一动点.
如图,在平面直角坐标系中,O是坐标原点,点A的坐标是(1,3),点P的坐标是(0,b)(b≠0).直线AP交x轴于点B,记点P关于x轴的对称点为P′,点Q为x轴上一动点.