Question

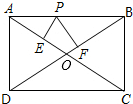在矩形ABCD中，AB=4，AD=3，P为AB上的动点，PE⊥AC于E，PF⊥BD于F，求PE+PF的值．

Answer 1

考点：矩形的性质

专题：

分析：过点A作AG⊥BD于G，连接PO，根据勾股定理列式求出BD的长度，再根据△ABD的面积求出AG，然后根据△AOB的面积求出PE+PF=AG，从而得解．

解答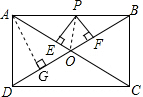：解：如图，过点A作AG⊥BD于G，连接PO，
∵AB=4，AD=3，
∴BD=

AB2+AD2

=

42+32

=5，
∴S_△ABD=

1

2

AB2+AD2

BD•AG=

1

2

AB•AD
即

1

2

×5•AG=

1

2

×3×4，
解得AG=2.4，
在矩形ABCD中，AO=OB，
∴S_△AOB=

1

2

AO•PE+

1

2

OB•PF=

1

2

OB•AG，
∴PE+PF=AG=2.4．即PE+PF=2.4．

点评：本题考查了矩形的对角线相等且互相平分的性质，勾股定理的应用，根据三角形的面积求出PE+PF=AG是解题的关键，作辅助线是难点．