题目内容
 已知,O为△ABC内的任一点,求证:
已知,O为△ABC内的任一点,求证:| 1 |
| 2 |
考点:三角形三边关系
专题:证明题
分析:先根据两边之和大于第三边得出
(AB+BC+CA)<OA+OB+OC,再根据两边之差小于第三边即可得出OA+OB+OC<AB+AC+BC即可.
| 1 |
| 2 |
解答:解:∵三角形中任意两边之和大于第三边,
∴OA+OB>AB,OA+OC>CA,OB+OC>BC,
∴2(OA+OB+OC)>AB+BC+CA,即
(AB+BC+CA)<OA+OB+OC;
∵三角形中任意两边之差小于第三边,
∴CA-CO<AO,BC-BO<CO,AB-AO<BO,
两边相加得,CA+AB+BC-(AO+BO+CO)<AO+BO+CO,即AC+AB+BC<2(AO+BO+CO)
∴AC+AB+BC>AO+BO+CO
∴
(AB+BC+CA)<OA+OB+OC<AB+AC+BC.
∴OA+OB>AB,OA+OC>CA,OB+OC>BC,
∴2(OA+OB+OC)>AB+BC+CA,即
| 1 |
| 2 |
∵三角形中任意两边之差小于第三边,
∴CA-CO<AO,BC-BO<CO,AB-AO<BO,
两边相加得,CA+AB+BC-(AO+BO+CO)<AO+BO+CO,即AC+AB+BC<2(AO+BO+CO)
∴AC+AB+BC>AO+BO+CO
∴
| 1 |
| 2 |
点评:本题考查的是三角形的三边关系,熟知三角形任意两边之和大于第三边,任意两边之差小于第三边是解答此题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
式子
有意义,则x的取值范围是( )
| x-3 |
| A、x=3 | B、x≥3 |
| C、x<3 | D、x>3 |
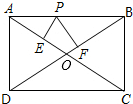 在矩形ABCD中,AB=4,AD=3,P为AB上的动点,PE⊥AC于E,PF⊥BD于F,求PE+PF的值.
在矩形ABCD中,AB=4,AD=3,P为AB上的动点,PE⊥AC于E,PF⊥BD于F,求PE+PF的值. 如图所示是n个小正方体搭成的几何体的俯视图,请分别画出它的主视图和左视图.
如图所示是n个小正方体搭成的几何体的俯视图,请分别画出它的主视图和左视图. 已知,如图,点B、C在线段AD上,AB=CD,EA⊥AD,BF⊥BD,CE=DF,求证:CE∥DF.
已知,如图,点B、C在线段AD上,AB=CD,EA⊥AD,BF⊥BD,CE=DF,求证:CE∥DF.