题目内容
当t取什么值时，关于x的一元二次方程2x2+tx+2=0有两个相等的实数根？并求出此时方程的根．
考点：根的判别式
专题：
分析：根据一元二次方程的根的判别式△=b2-4ac=0列出关于t的一元二次方程，然后解方程即可．
解答：解：∵一元二次方程2x2+tx+2=0有两个相等的实数根，
∴△=t2-4×2×2=t2-16=0，
解得，t=±4，
∴当t=4或t=-4时，原方程有两个相等的实数根．；
当t=4，原方程变为：2x2+4x+2=0，2（x+1）2=0，解得x1=x2=-1；
当t=-4，原方程变为：2x2-4x+2=0，2（x-1）2=0，解得x1=x2=1．
∴△=t2-4×2×2=t2-16=0，
解得，t=±4，
∴当t=4或t=-4时，原方程有两个相等的实数根．；
当t=4，原方程变为：2x2+4x+2=0，2（x+1）2=0，解得x1=x2=-1；
当t=-4，原方程变为：2x2-4x+2=0，2（x-1）2=0，解得x1=x2=1．
点评：本题考查了一元二次方程的根与系数的关系．当△=b2-4ac＞0时，方程有两个不相等的实数根；当△=b2-4ac=0时，方程有两个相等的实数根；△=b2-4ac＜0时，方程无实数根．
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
下列根式中，能与
合并的二次根式是（ ）
| 3 |
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
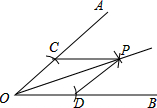用尺规作图作∠AOB的平分线的方法如下：以O为圆心，任意长为半径画弧交OA，OB于点C，D，再分别以点C，D为圆心，以大于
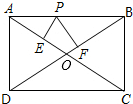在矩形ABCD中，AB=4，AD=3，P为AB上的动点，PE⊥AC于E，PF⊥BD于F，求PE+PF的值．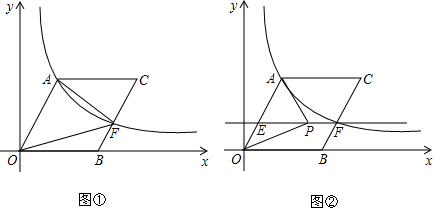
如图所示是n个小正方体搭成的几何体的俯视图，请分别画出它的主视图和左视图．
抛物线y=ax2+ax+c（a≠0）与x轴交于A、B两点（A在B的左边），与y轴交于点C，AB=3，且抛物线过点P（-1，3），求抛物线的解析式．