题目内容
 如图,在矩形ABCD中,BE平分∠ABC交AD于点E,若∠EBO=15°,求∠AOE的度数.
如图,在矩形ABCD中,BE平分∠ABC交AD于点E,若∠EBO=15°,求∠AOE的度数.考点:矩形的性质
专题:
分析:利用矩形的性质和角平分线的性质可知∠AEB=∠CBE=45°,则∠3=∠AEB-∠1=30°;通过∠3=30°,∠BAO=60°证得△AOB为等边三角形,结合AB=AE可得AO=AE.
解答: 解:如图,∵在矩形ABCD中,BE平分∠ABC,∠1=15°,
解:如图,∵在矩形ABCD中,BE平分∠ABC,∠1=15°,
∴∠AEB=∠CBE=45°,
∴∠3=∠AEB-∠1=30°,AB=AE,
∴∠ABO=60°.
∵OA=OB,
∴△OAB是等边三角形.
∴OA=AB,∠OAB=60°,
∴OA=AE,∠OAE=30°,
∠2=
=75°.即∠AOE=75°.
 解:如图,∵在矩形ABCD中,BE平分∠ABC,∠1=15°,
解:如图,∵在矩形ABCD中,BE平分∠ABC,∠1=15°,∴∠AEB=∠CBE=45°,
∴∠3=∠AEB-∠1=30°,AB=AE,
∴∠ABO=60°.
∵OA=OB,
∴△OAB是等边三角形.
∴OA=AB,∠OAB=60°,
∴OA=AE,∠OAE=30°,
∠2=
| 180°-30° |
| 2 |
点评:主要考查了等边三角形的性质和矩形的性质.解题的关键是要知道:矩形的两条对角线互相平分且相等.

练习册系列答案
相关题目
下列二次根式中,与
是同类二次根式的是( )
| 3 |
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
 往返于甲、乙两地的客车,中途有三个站.其中每两站的票价不同.问:
往返于甲、乙两地的客车,中途有三个站.其中每两站的票价不同.问: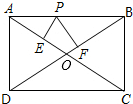 在矩形ABCD中,AB=4,AD=3,P为AB上的动点,PE⊥AC于E,PF⊥BD于F,求PE+PF的值.
在矩形ABCD中,AB=4,AD=3,P为AB上的动点,PE⊥AC于E,PF⊥BD于F,求PE+PF的值. 如图所示,M是弧AB的中点,OM是⊙O 半径交弦AB于点N,AB=4
如图所示,M是弧AB的中点,OM是⊙O 半径交弦AB于点N,AB=4 如图所示是n个小正方体搭成的几何体的俯视图,请分别画出它的主视图和左视图.
如图所示是n个小正方体搭成的几何体的俯视图,请分别画出它的主视图和左视图.