题目内容
古代阿拉伯数学家泰比特·伊本·奎拉对勾股定理进行了推广研究:如图(图1中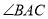 为锐角,图2中
为锐角,图2中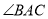 为直角,图3中
为直角,图3中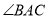 为钝角).
为钝角).
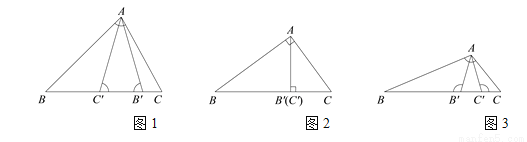
在△ABC的边BC上取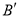 ,
, 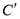 两点,使
两点,使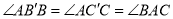 ,则
,则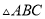 ∽
∽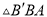 ∽
∽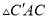 ,
, 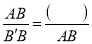 ,
, 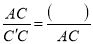 ,进而可得
,进而可得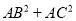
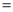 ;(用
;(用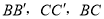 表示)
表示)
若AB=4,AC=3,BC=6,则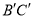
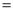 .
.
练习册系列答案
相关题目
题目内容
古代阿拉伯数学家泰比特·伊本·奎拉对勾股定理进行了推广研究:如图(图1中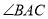 为锐角,图2中
为锐角,图2中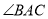 为直角,图3中
为直角,图3中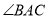 为钝角).
为钝角).

在△ABC的边BC上取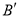 ,
, 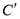 两点,使
两点,使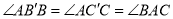 ,则
,则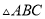 ∽
∽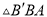 ∽
∽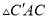 ,
, 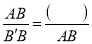 ,
, 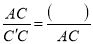 ,进而可得
,进而可得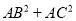
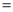 ;(用
;(用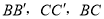 表示)
表示)
若AB=4,AC=3,BC=6,则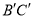
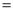 .
.