题目内容
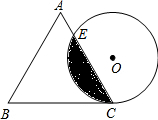 如图,边长为4cm的等边三角形ABC与⊙O等高(即高与直径相等),⊙O与BC相切于点C,⊙O与AC相交于E.
如图,边长为4cm的等边三角形ABC与⊙O等高(即高与直径相等),⊙O与BC相切于点C,⊙O与AC相交于E.求:(1)CE的长;(2)阴影部分的面积.
考点:切线的性质,等边三角形的性质,扇形面积的计算
专题:
分析:(1)由等边三角形ABC求出⊙O的直径,得出半径OC的长,在Rt△OCF中求出CF的长得出CE的长;
(2)阴影部分的面积=扇形的面积-△OCE的面积.
(2)阴影部分的面积=扇形的面积-△OCE的面积.
解答:解:(1)连接OC、OE,作OF⊥CE于F,作AD⊥BC于D,如图所示: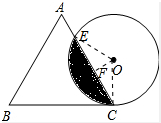
∵⊙O与BC相切于点C,
∴∠BCO=90°,
∵△ABC是等边三角形,
∴∠ACB=60°,AB=BC=4,
∴∠OCF=90°-60°=30°,BD=CD=2,AD=
=2
,
∴OC=
AD=
,
∴OF=
OC=
,
∴CF=1,
∵OF⊥CE,
∴CE=2CF=2;
(2)S扇形OCE-S△OCE=
-
×3×
=π-
.

∵⊙O与BC相切于点C,
∴∠BCO=90°,
∵△ABC是等边三角形,
∴∠ACB=60°,AB=BC=4,
∴∠OCF=90°-60°=30°,BD=CD=2,AD=
| 42-22 |
| 3 |
∴OC=
| 1 |
| 2 |
| 3 |
∴OF=
| 1 |
| 2 |
| ||
| 2 |
∴CF=1,
∵OF⊥CE,
∴CE=2CF=2;
(2)S扇形OCE-S△OCE=
120π•(
| ||
| 360 |
| 1 |
| 2 |
| ||
| 2 |
3
| ||
| 4 |
点评:本题考查了等边三角形的性质、切线的性质以及扇形面积的计算方法;主要培养学生综合运用有关定理进行推理计算的能力.

练习册系列答案
 同步轻松练习系列答案
同步轻松练习系列答案 课课通课程标准思维方法与能力训练系列答案
课课通课程标准思维方法与能力训练系列答案
相关题目
 如图中的△A′B′C′是由△ABC绕点P旋转180°后得到的图形,根据旋转的性质回答下列问题:
如图中的△A′B′C′是由△ABC绕点P旋转180°后得到的图形,根据旋转的性质回答下列问题: 已知Rt△ABC中,∠ACB=90°,CA=CB,有一个圆心角为45°,半径的长等于CA的扇形CEF绕点C旋转,且直线CE,CF分别与直线AB交于点M,N当扇形CEF绕点C在∠ACB的内部旋转时,如图,求证:MN2=AM2+BN2.
已知Rt△ABC中,∠ACB=90°,CA=CB,有一个圆心角为45°,半径的长等于CA的扇形CEF绕点C旋转,且直线CE,CF分别与直线AB交于点M,N当扇形CEF绕点C在∠ACB的内部旋转时,如图,求证:MN2=AM2+BN2. 如图,正比例函数y=2x的图象与反比例函数y=
如图,正比例函数y=2x的图象与反比例函数y=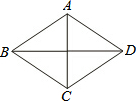 如图,在菱形ABCD中,AC=6,BD=8.
如图,在菱形ABCD中,AC=6,BD=8. 如图所示,CE是BC的延长线.
如图所示,CE是BC的延长线. 在正方形ABCD中,O是对角线AC、BD的交点,分别过点A、B、C、D作BD、AC的平行线交于点E、F、G、H.
在正方形ABCD中,O是对角线AC、BD的交点,分别过点A、B、C、D作BD、AC的平行线交于点E、F、G、H.