题目内容
 如图,△ABC与△CDE都是正三角形,图中可以通过旋转而相互得到到的三角形是
如图,△ABC与△CDE都是正三角形,图中可以通过旋转而相互得到到的三角形是考点:旋转的性质
专题:
分析:如图,根据题意证明△ACD≌△BCE,结合旋转变换的定义,即可解决问题.
解答: 解:如图,∵△ABC与△CDE都是正三角形,
解:如图,∵△ABC与△CDE都是正三角形,
∴AC=BC,DC=EC;∠ACB=∠DCE=60°,
∴∠ACD=∠BCE;
在△ACD与△BCE中,
,
∴△ACD≌△BCE(SAS),
∴图中可以通过旋转而相互得到到的三角形是△ACD、△BCE;旋转角的度数是60°.
故答案为△ACD、△BCE;60°.
 解:如图,∵△ABC与△CDE都是正三角形,
解:如图,∵△ABC与△CDE都是正三角形,∴AC=BC,DC=EC;∠ACB=∠DCE=60°,
∴∠ACD=∠BCE;
在△ACD与△BCE中,
|
∴△ACD≌△BCE(SAS),
∴图中可以通过旋转而相互得到到的三角形是△ACD、△BCE;旋转角的度数是60°.
故答案为△ACD、△BCE;60°.
点评:该题主要考查了旋转变换的定义及其应用问题;解题的关键是首先根据旋转变换的定义及其性质,找出图中的全等三角形.

练习册系列答案
相关题目
 A、B、C、D是直线上顺次四点,AB、BC和CD的长度比为2:3:4,点E、F分别是AB、CD的中点,且EF=4.8cm,求AB的长.
A、B、C、D是直线上顺次四点,AB、BC和CD的长度比为2:3:4,点E、F分别是AB、CD的中点,且EF=4.8cm,求AB的长.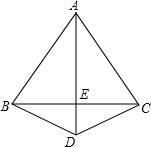 如图,AB=AC=8cm,DB=DC,若∠ABC=60°,则BE=
如图,AB=AC=8cm,DB=DC,若∠ABC=60°,则BE= 如图,正比例函数y=2x的图象与反比例函数y=
如图,正比例函数y=2x的图象与反比例函数y= 如图,矩形OABC的顶点A,C分别在x,y轴的正半轴上,点D为对角线OB的中点,点E(4,n)在边AB上,反比例函数y=
如图,矩形OABC的顶点A,C分别在x,y轴的正半轴上,点D为对角线OB的中点,点E(4,n)在边AB上,反比例函数y=