题目内容
17.如图1,已知在梯形ABCD中,AD∥BC,AB=DC=5,AD=4,M、N分别是边AD、BC上的任意一点,联结AN、DN,点E、F分别在线段AN、DN上,且ME∥DN,MF∥AN,联结EF.(1)如图2,如果EF∥BC,求EF的长;
(2)如果四边形MENF的面积是△ADN的面积的$\frac{3}{8}$,求AM的长;
(3)如果BC=10,试探索△ABN、△AND、△DNC能否两两相似?如果能,求AN的长;如果不能,请说明理由.
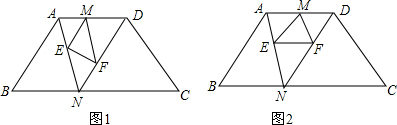
分析 (1)利用平行线分线段成比例得到EF是△AND的中位线,利用三角形中位线定理进行解答即可;
(2)设AM=x.利用(1)中相似三角形的性质得到$\frac{{S}_{△AME}}{{S}_{△ADN}}$=$(\frac{AM}{AD})^{2}$=$\frac{{x}^{2}}{16}$,$\frac{{{S}_{△}}_{DMF}}{{S}_{△ADN}}$=$(\frac{DM}{AD})^{2}$=$\frac{(4-x)^{2}}{16}$,利用图中相关图形的面积间的数量关系和已知条件列出关于x的方程[1-$\frac{{x}^{2}}{16}$-$\frac{(4-x)^{2}}{16}$]S△AND=$\frac{3}{2}$S△AND.由此求得x的值;
(3)如答图2,过点A作AP⊥BC于P,过点D作DQ⊥BC于Q.需要分类讨论:当△ABN∽△DCN、△ABN∽△NCD两种情况,利用相似三角形的对应边成比例求得BN=CN=5,然后利用勾股定理计算AM的长度.
解答 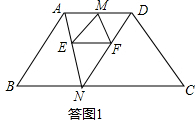 解:(1)如答图1,∵EF∥BC,AD∥BC,
解:(1)如答图1,∵EF∥BC,AD∥BC,
∴EF∥AD,
又∵ME∥DN,MF∥AN,
∴$\frac{NE}{AN}$=$\frac{FN}{ND}$=$\frac{AM}{AD}$=$\frac{AE}{AN}$,
∴AE=EN.
同理,NF=FD,
∴EF是△AND的中位线,
∴EF=$\frac{1}{2}$AD=2;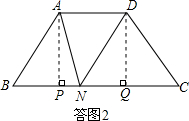
(2)设AM=x.
则$\frac{{S}_{△AME}}{{S}_{△ADN}}$=$(\frac{AM}{AD})^{2}$=$\frac{{x}^{2}}{16}$,$\frac{{{S}_{△}}_{DMF}}{{S}_{△ADN}}$=$(\frac{DM}{AD})^{2}$=$\frac{(4-x)^{2}}{16}$,
∴S四边形MENF=[1-$\frac{{x}^{2}}{16}$-$\frac{(4-x)^{2}}{16}$]S△AND=$\frac{3}{8}$S△AND.
解得 x1=1,x2=3,
∴AM的长度是1或3;
(3)如答图2,过点A作AP⊥BC于P,过点D作DQ⊥BC于Q,
则PQ=AD=4,BP=CQ=3.
当△ABN∽△DCN时,$\frac{AB}{CD}$=$\frac{BN}{CN}$=1,
∴BN=CN=5.
∴DN=AN=$\sqrt{A{P}^{2}+N{P}^{2}}$=$2\sqrt{5}$.
又$\frac{AD}{AN}$=$\frac{AN}{AB}$=$\frac{DN}{BN}$=$\frac{2\sqrt{5}}{5}$,
∴△NAD∽△BAN∽△CDN.
当△ABN∽△NCD时,$\frac{AB}{CN}$=$\frac{BN}{CD}$,
解得BN=CN=5,
∴DN=AN=$\sqrt{A{P}^{2}+N{P}^{2}}$=2$\sqrt{5}$.
综上所述,当△ABN、△AND、△DNC两两相似时,AN=$2\sqrt{5}$.
点评 本题考查了相似综合题.该题综合性比较强,涉及到了三角形中位线定理,相似三角形的判定与性质,勾股定理等知识点,解题时,运用了“数形结合”和“分类讨论”的数学思想.

 阅读快车系列答案
阅读快车系列答案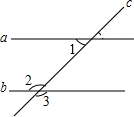 如图,a∥b,∠3=135°,则∠1的度数是( )
如图,a∥b,∠3=135°,则∠1的度数是( )| A. | 45° | B. | 55° | C. | 65° | D. | 75° |

| A. | 2≤l≤2$\sqrt{3}$ | B. | 3≤l≤3$\sqrt{3}$ | C. | 3$\sqrt{3}$≤l≤6$\sqrt{3}$ | D. | 6$≤l≤6\sqrt{3}$ |
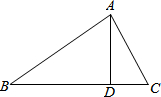 如图,点D在线段BC上,已知∠BAC=90°,∠DAC+∠C=90°,则∠BAD和∠C的大小关系是∠BAD=∠C,其依据是同角的余角相等.
如图,点D在线段BC上,已知∠BAC=90°,∠DAC+∠C=90°,则∠BAD和∠C的大小关系是∠BAD=∠C,其依据是同角的余角相等.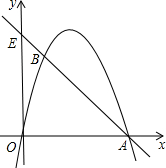 在如图所示的平面直角坐标系中,直线y=-x+8与x轴、y轴分别交于A、E两点,点B在线段AE上,且AB=6$\sqrt{2}$.
在如图所示的平面直角坐标系中,直线y=-x+8与x轴、y轴分别交于A、E两点,点B在线段AE上,且AB=6$\sqrt{2}$.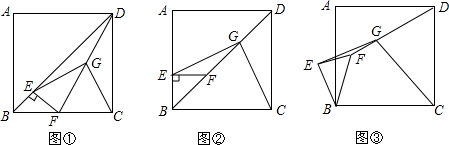
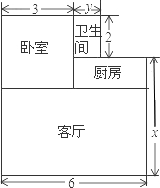 老李购买了一套学位房,他准备将地面铺上地砖,地面结构如图所示.
老李购买了一套学位房,他准备将地面铺上地砖,地面结构如图所示.