题目内容
在图中，一次函数y=x-2与反比例函数y=| 3 |
| x |
| A、x＜-1或0＜x＜2 |
| B、x＜-1或 0＜x＜3 |
| C、-1＜x＜0或0＜x＜3 |
| D、x＞-1或0＜x＜2 |
考点：反比例函数与一次函数的交点问题
专题：计算题
分析：先根据反比例函数与一次函数的交点问题确定交点坐标，然后观察函数图象得到当x＜-1或0＜x＜3时，一次函数图象都在反比例函数图象下方．
解答：解：解方程组
得
或
，
所以A点坐标为（-1，3），B点坐标为（3，1），
当x＜-1或0＜x＜3时，一次函数值小于反比例函数值．
故选B．
|
|
|
所以A点坐标为（-1，3），B点坐标为（3，1），
当x＜-1或0＜x＜3时，一次函数值小于反比例函数值．
故选B．
点评：本题考查了反比例函数与一次函数的交点问题：反比例函数与一次函数图象的交点坐标满足两函数解析式．
练习册系列答案
相关题目
点P（a，2）与点Q（3，b）是抛物线y=x2-2x+c上两点，且点P、Q关于此抛物线的对称轴对称，则ab的值为（ ）
| A、1 | B、-1 | C、-2 | D、2 |
若a=(
)-2，b=(-1)-1，c=(-
)0，则a、b、c的大小关系是（ ）
| 1 |
| 2 |
| π |
| 2 |
| A、a＞b＞c |
| B、a＞c＞b |
| C、c＞a＞b |
| D、c＞b＞a |
样本容量为200的频率分布直方图如图．根据样本的频率分布直方图估计，样本数据落在[6，10）内的频数为（ ）| A、32 | B、36 | C、46 | D、64 |
如图，在△ABC中，已知∠C=90°，AC=8，BC=6，D是AC中点，过点D作DE⊥AB于E，求DE的长．
如图，每个小正方形的边长都是1．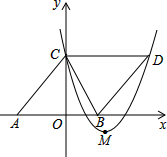
如图，在平面直角坐标系xOy中，菱形ABDC的边AB在x轴上，顶点C在y轴上，A（-6，0），C（0，8），抛物线y=ax2-10ax+c经过点C，且顶点M在直线BC上，则抛物线解析式为