题目内容
把几个数用大括号围起来,中间用逗号断开,如:{1,2,-3}、{-2,7,
,19},我们称之为集合,其中的数称其为集合的元素.如果一个集合满足:当实数a是集合的元素时,实数6-a也必是这个集合的元素,这样的集合我们称为好的集合.
(1)请你判断集合{1,2},{-2,1,3,5,8}是不是好的集合?
(2)请你写出满足条件的两个好的集合的例子.
| 3 |
| 4 |
(1)请你判断集合{1,2},{-2,1,3,5,8}是不是好的集合?
(2)请你写出满足条件的两个好的集合的例子.
考点:实数
专题:新定义
分析:(1)本题中给出了判定好,坏集合的条件,即:集合中两个数的和等于8或某个数的2倍等于8时集合时好集合,反之是坏集合,那么可按有理数的减法,让8减去集合中的某一个数,看看得出的结果是否在该集合中即可,如果在则是好集合,如果不在就不是好集合;
(2)根据题意写出符合的好的集合即可.
(2)根据题意写出符合的好的集合即可.
解答:解:(1)集合{1,2}不是好的集合,
这是因6-1=5,而5不是{1,2}中的数,
所以{1,2}不是好的集合,
{-2,1,3,5,8}是好的集合,
这是因为6-1=5,6-(-2)=8,6-3=3,6-5=1,6-8=-2
5、8、3、1、-2都是{-2,1,3,5,8}中的数,
所以{-2,1,3,5,8}是好的集合;
(2)答案不唯一,集合{4,2}、{1,5}等都是好的集合.
这是因6-1=5,而5不是{1,2}中的数,
所以{1,2}不是好的集合,
{-2,1,3,5,8}是好的集合,
这是因为6-1=5,6-(-2)=8,6-3=3,6-5=1,6-8=-2
5、8、3、1、-2都是{-2,1,3,5,8}中的数,
所以{-2,1,3,5,8}是好的集合;
(2)答案不唯一,集合{4,2}、{1,5}等都是好的集合.
点评:本题考查了有理数的加减的应用,要读懂题意,根据有理数的减法按照题中给出的判断条件进行求解即可.

练习册系列答案
 快乐5加2金卷系列答案
快乐5加2金卷系列答案
相关题目
顺次连接一个四边形的各边中点,得到了一个矩形,则下列四边形满足条件的是( )
①平行四边形;②菱形;③对角线互相垂直的四边形.
①平行四边形;②菱形;③对角线互相垂直的四边形.
| A、①③ | B、②③ | C、①② | D、均可以 |
一棵大树被台风刮断,若树在离地面4米处折断,树顶端落在离树底部3米处,则树折断之前有( )
| A、5米 | B、7米 | C、8米 | D、9米 |
 在图中,一次函数y=x-2与反比例函数y=
在图中,一次函数y=x-2与反比例函数y=| 3 |
| x |
| A、x<-1或0<x<2 |
| B、x<-1或 0<x<3 |
| C、-1<x<0或0<x<3 |
| D、x>-1或0<x<2 |
 (1)如图,从一个直径是
(1)如图,从一个直径是
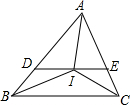 如图,△ABC中,IB,IC分别平分∠ABC,∠ACB,过I点作DE∥BC,分别交AB于D,交AC于E,给出下列结论:
如图,△ABC中,IB,IC分别平分∠ABC,∠ACB,过I点作DE∥BC,分别交AB于D,交AC于E,给出下列结论: