题目内容
15．
如图，在△ABC中，BD是∠ABC的平分线，EF垂直平分BD．求证：∠ABD=∠BDF．
分析 根据线段垂直平分线的性质得到FB=FD，由等腰三角形的性质得到∠FBD=∠BDF，根据角平分线的定义得到∠ABD=∠FBD，等量代换即可得到结论．
解答 证明：∵EF垂直平分BD，
∴FB=FD，
∴∠FBD=∠BDF，
∵BD是∠ABC的平分线，
∴∠ABD=∠FBD，
∴∠ABD=∠BDF．
点评 本题考查了线段垂直平分线的性质，角平分线的定义，熟练掌握线段垂直平分线的性质是解题的关键．
练习册系列答案
相关题目
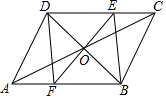在一次数学课上，张老师出示了一个题目：“如图，?ABCD的对角线相交于点O，过点O作EF垂直于BD交AB，CD分别于点F，E，连接DF，BE．请根据上述条件，写出一个正确结论．”其中四位同学写出的结论如下：
如图，在矩形ABCD中，点E是BC上一点，且DE=DA，AF⊥DE于F，求证：AF=CD．
如图，小明要测量河内小岛B到河边公路AD的距离，在点A处测得∠BAD=37°，沿AD方向前进150米到达点C，测得∠BCD=45°．求小岛B到河边公路AD的距离．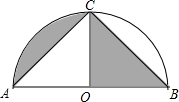
如图，以点O为圆心的半圆经过点C，AB为直径，若AC=BC=$\sqrt{2}$，则图中阴影部分的面积是$\frac{π}{4}$．