题目内容
15.在△ABC中,AB=AC,点D为射线BC上一个动点(不与B、C重合),以AD为一边向AD的左侧作△ADE,使AD=AE,∠DAE=∠BAC,过点E作BC的平行线,交直线AB于点F,连接BE.(1)如图1,当点D在线段BC上移动;
①求证:△ABE≌△ACD;
②求证:△BEF是等腰三角形;
(2)如图2,当点D在线段BC的延长线上移动,请在图中画出相应的图形.
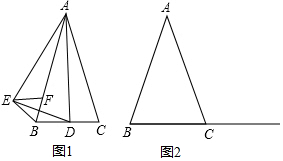
分析 (1)①证明∠BAE=∠DAC,根据全等三角形的判定定理证明;
②根据全等三角形的性质得到∠ABE=∠ACD,根据等腰三角形的性质得到∠ABC=∠ACD,根据平行线的性质、等腰三角形的判定定理证明;
(2)根据题意画出图形即可.
解答 (1)①证明:∵∠DAE=∠BAC,
∴∠DAE-∠DAB=∠BAC-∠DAB,即∠BAE=∠DAC,
在△ABE和△ACD中,
$\left\{\begin{array}{l}{AE=AD}\\{∠BAE=∠CAD}\\{AB=AC}\end{array}\right.$,
∴△ABE≌△ACD;
②证明:∵△ABE≌△ACD,
∴∠ABE=∠ACD,
∵AB=AC,
∴∠ABC=∠ACD,
∵EF∥BC,
∴∠ABC=∠EFB,
∴∠ABE=∠EFB,
∴EB=EF,即△BEF是等腰三角形;
(2)如图所示2即为所求.
点评 本题考查的是等腰三角形的性质、全等三角形的判定和性质,掌握全等三角形的判定定理和性质定理、等腰三角形的性质定理是解题的关键.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
17.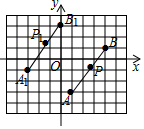 如图,线段AB经过平移得到线段A1B1,其中A、B的对应点分别为A1、B1,这四个点都在格点上,若线段AB上有一个点P(a,b),则点P在A1B1上的对应点P1的坐标为( )
如图,线段AB经过平移得到线段A1B1,其中A、B的对应点分别为A1、B1,这四个点都在格点上,若线段AB上有一个点P(a,b),则点P在A1B1上的对应点P1的坐标为( )
 如图,线段AB经过平移得到线段A1B1,其中A、B的对应点分别为A1、B1,这四个点都在格点上,若线段AB上有一个点P(a,b),则点P在A1B1上的对应点P1的坐标为( )
如图,线段AB经过平移得到线段A1B1,其中A、B的对应点分别为A1、B1,这四个点都在格点上,若线段AB上有一个点P(a,b),则点P在A1B1上的对应点P1的坐标为( )| A. | (a-4,b+2) | B. | (a-4,b-2) | C. | (a+4,b+2) | D. | (a+4,b-2) |
3.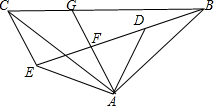 如图,△ABC和△ADE均为等腰直角三角形,∠BAC=∠DAE=90°,点B,D,E在同一直线上,AG是∠DAE的平分线,分别交DE,BC于点F,G,连接CE,∠GAC=25°,所给结论:①∠BAD=∠CAE;②tan∠ABE=$\frac{\sqrt{3}}{3}$;③AG∥CE;④2AF+CE=BE;⑤AD=CG中,正确的有( )
如图,△ABC和△ADE均为等腰直角三角形,∠BAC=∠DAE=90°,点B,D,E在同一直线上,AG是∠DAE的平分线,分别交DE,BC于点F,G,连接CE,∠GAC=25°,所给结论:①∠BAD=∠CAE;②tan∠ABE=$\frac{\sqrt{3}}{3}$;③AG∥CE;④2AF+CE=BE;⑤AD=CG中,正确的有( )
 如图,△ABC和△ADE均为等腰直角三角形,∠BAC=∠DAE=90°,点B,D,E在同一直线上,AG是∠DAE的平分线,分别交DE,BC于点F,G,连接CE,∠GAC=25°,所给结论:①∠BAD=∠CAE;②tan∠ABE=$\frac{\sqrt{3}}{3}$;③AG∥CE;④2AF+CE=BE;⑤AD=CG中,正确的有( )
如图,△ABC和△ADE均为等腰直角三角形,∠BAC=∠DAE=90°,点B,D,E在同一直线上,AG是∠DAE的平分线,分别交DE,BC于点F,G,连接CE,∠GAC=25°,所给结论:①∠BAD=∠CAE;②tan∠ABE=$\frac{\sqrt{3}}{3}$;③AG∥CE;④2AF+CE=BE;⑤AD=CG中,正确的有( )| A. | ①③⑤ | B. | ②③④ | C. | ①②④ | D. | ①③④ |
20.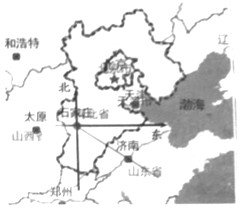 如图,济南大约位于石家庄的南偏东56°方向上,则石家庄大约位于济南的( )
如图,济南大约位于石家庄的南偏东56°方向上,则石家庄大约位于济南的( )
 如图,济南大约位于石家庄的南偏东56°方向上,则石家庄大约位于济南的( )
如图,济南大约位于石家庄的南偏东56°方向上,则石家庄大约位于济南的( )| A. | 北偏西56°方向上 | B. | 北偏西34°方向上 | C. | 南偏西34°方向上 | D. | 南偏东56°方向上 |
5.下列计算正确的是( )
| A. | 2mn+3mn=6mn | B. | mn2+mn3=mn5 | C. | mn3÷mn2=n | D. | (mn3)2=m2n5 |
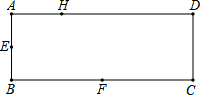 如图,矩形ABCD的长和宽分别为3和1,点E、F分别是AB、BC边的中点,点H在矩形ABCD边上,则使△EFH为直角三角形的点H的个数为( )
如图,矩形ABCD的长和宽分别为3和1,点E、F分别是AB、BC边的中点,点H在矩形ABCD边上,则使△EFH为直角三角形的点H的个数为( ) 如图使用五个相同的立方体搭成的几何体,从正面看的图形是( )
如图使用五个相同的立方体搭成的几何体,从正面看的图形是( )



 如图,在△ABC中,AB=AC,∠A=36°,线段AB的垂直平分线MN分别交AB、AC于N、M.
如图,在△ABC中,AB=AC,∠A=36°,线段AB的垂直平分线MN分别交AB、AC于N、M.