Question

5．提出问题：当x＞0时如何求函数y=x+$\frac{1}{x}$的最大值或最小值？
分析问题：前面我们刚刚学过二次函数的相关知识，知道求二次函数的最值时，我们可以利用它的图象进行猜想最值，或利用配方可以求出它的最值．
例如我们求函数y=x-2$\sqrt{x}$（x＞0）的最值时，就可以仿照二次函数利用配方求最值的方法解决问题；y=x-2$\sqrt{x}$=（$\sqrt{x}$）²-2$\sqrt{x}$-2$\sqrt{x}$+1-1=（$\sqrt{x}$-1）²-1即当x=1时，y有最小值为-1
解决问题
借鉴我们已有的研究函数的经验，探索函数y=x+$\frac{1}{x}$（x＞0）的最大（小）值．
（1）实践操作：填写下表，并用描点法画出函数y=x+$\frac{1}{x}$（x＞0）的图象：

x	…	$\frac{1}{4}$	$\frac{1}{3}$	$\frac{1}{2}$	1	2	3	4	…
y	…								…

（2）观察猜想：观察该函数的图象，猜想
当x=1时，函数y=x+$\frac{1}{x}$（x＞0）有最小值（填“大”或“小”），是2．
（3）推理论证：利用上述例题，请你尝试通过配方法求函数y=x+$\frac{1}{x}$（x＞0）的最大（小）值，以证明你的猜想．知识能力运用：直接写出函数y=-2x-$\frac{1}{2x}$（x＞0）当x=$\frac{1}{2}$时，该函数有最大值（填“大”或“小”），是-2．

Answer 1

分析 （1）由x的值计算出y的值，填表即可；用描点法画出图象即可；
（2）用配方法得出y=x+$\frac{1}{x}$=（$\sqrt{x}$-$\frac{1}{\sqrt{x}}$）²+2，即可得出结果；
（3）用配方法得出y=-2x-$\frac{1}{2x}$=-（$\sqrt{2x}$-$\frac{1}{\sqrt{2x}}$）²-2，即可得出结果．

解答 解：（1）当x=$\frac{1}{4}$时，y=x+$\frac{1}{x}$=$\frac{1}{4}$+4=4$\frac{1}{4}$；
当x=$\frac{1}{3}$时，y=x+$\frac{1}{x}$=$\frac{1}{3}$+3=3$\frac{1}{3}$；
当x=$\frac{1}{2}$时，y=x+$\frac{1}{x}$=$\frac{1}{2}$+2=2$\frac{1}{2}$；
当x=1时，y=x+$\frac{1}{x}$=1+1=2；
当x=2时，y=x+$\frac{1}{x}$=2+$\frac{1}{2}$=2$\frac{1}{2}$；
当x=3时，y=x+$\frac{1}{x}$=3+$\frac{1}{3}$=3$\frac{1}{3}$；
当x=4时，y=x+$\frac{1}{x}$=4+$\frac{1}{4}$=4$\frac{1}{4}$；填表如下：
函数图象如图所示：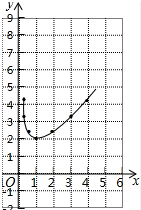
（2）∵y=x+$\frac{1}{x}$=（$\sqrt{x}$）²+（$\frac{1}{\sqrt{x}}$）²=（$\sqrt{x}$-$\frac{1}{\sqrt{x}}$）²+2，
∴当x=1时，函数y=x+$\frac{1}{x}$（x＞0）有最小值，最小值为2；
故答案为：1，小，2；
（3）∵y=-2x-$\frac{1}{2x}$=-（2x+$\frac{1}{2x}$）=-（$\sqrt{2x}$-$\frac{1}{\sqrt{2x}}$）²-2，
∴当$\sqrt{2x}$=1，即x=$\frac{1}{2}$时，函数y=-2x-$\frac{1}{2x}$（x＞0）有最大值，最大值为-2；
故答案为：$\frac{1}{2}$，大，-2．

点评 本题是函数综合题目，考查了用描点法画函数的图象、函数的最值问题、配方法的应用；本题综合性强，难度较大，用配方法求出函数的最值是解决问题的关键．