题目内容
13．我们把三角形三边上的高产生的三个垂足组成的三角形称为该三角形的垂足三角形．已知等腰三角形的腰长为5，底边长为6，则该三角形的垂足三角形的周长是（ ）| A． | 8 | B． | 9 | C． | $\frac{192}{25}$ | D． | $\frac{112}{25}$ |
分析 根据直角三角形斜边上的中线等于斜边的一半，可得DF与BC的关系，DE与BC的关系，根据相似三角形的性质，可得EF的长，根据三角形的周长，可得答案．
解答 解：AD⊥BC，CE⊥AB，BF⊥AC，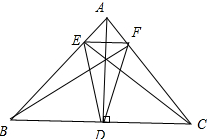
BD=CD，
∴DF=$\frac{1}{2}$BC=3，DE=$\frac{1}{2}$BC=3，
设AE=x，由勾股定理得
AB2-AF2=BC2-CF2
52-x2=62-（5-x）2，
x=$\frac{7}{5}$，
∵△AEF∽△ABC，
∴$\frac{AE}{AB}$=$\frac{EF}{BC}$，即$\frac{\frac{7}{5}}{5}$=$\frac{EF}{6}$，
解得EF=$\frac{42}{25}$，
∴该三角形的垂足三角形的周长是：3+3+$\frac{42}{25}$=$\frac{192}{25}$．
故选：C．
点评 本题考查了相似三角形的判定与性质以及直角三角形的性质，掌握直角三角形斜边上的中线等于斜边的一半、相似三角形的判定定理和性质定理是解题的关键．
练习册系列答案
优生乐园系列答案
新编小学单元自测题系列答案
相关题目
如图，丁丁做一道连线题，由于他不知道各种牙齿的作用，采取一一对应的方式随机连线答题．丁丁答题完全正确的概率是$\frac{1}{6}$．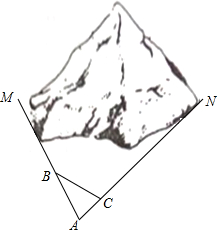
如图，M、N为山两侧的两个村庄，为了两村交通方便，根据国家的惠民政策，政府决定打一直线涵洞．工程人员为了计算工程量，必须计算M、N两点之间的直线距离，选择测量点A、B、C，点B、C分别在AM、AN上，现测得AM=1千米、AN=1.8千米，AB=54米、BC=45米、AC=30米，求M、N两点之间的直线距离．
如图，在边长为1个单位长度的小正方形组成的网格中，△ABC的顶点A、B、C在小正方形的顶点上，将△ABC向下平移4个单位、再向右平移3个单位得到△A1B1C1，然后将△A1B1C1绕点A1顺时针旋转90°得到△A1B2C2．
如图，已知AD是⊙O的直径，AB、BC是⊙O的弦，AD⊥BC，垂足是点E，BC=8，DE=2，求⊙O的半径长和sin∠BAD的值．
5．
提出问题：当x＞0时如何求函数y=x+$\frac{1}{x}$的最大值或最小值？
分析问题：前面我们刚刚学过二次函数的相关知识，知道求二次函数的最值时，我们可以利用它的图象进行猜想最值，或利用配方可以求出它的最值．
例如我们求函数y=x-2$\sqrt{x}$（x＞0）的最值时，就可以仿照二次函数利用配方求最值的方法解决问题；y=x-2$\sqrt{x}$=（$\sqrt{x}$）2-2$\sqrt{x}$-2$\sqrt{x}$+1-1=（$\sqrt{x}$-1）2-1即当x=1时，y有最小值为-1
解决问题
借鉴我们已有的研究函数的经验，探索函数y=x+$\frac{1}{x}$（x＞0）的最大（小）值．
（1）实践操作：填写下表，并用描点法画出函数y=x+$\frac{1}{x}$（x＞0）的图象：
（2）观察猜想：观察该函数的图象，猜想
当x=1时，函数y=x+$\frac{1}{x}$（x＞0）有最小值（填“大”或“小”），是2．
（3）推理论证：利用上述例题，请你尝试通过配方法求函数y=x+$\frac{1}{x}$（x＞0）的最大（小）值，以证明你的猜想．知识能力运用：直接写出函数y=-2x-$\frac{1}{2x}$（x＞0）当x=$\frac{1}{2}$时，该函数有最大值（填“大”或“小”），是-2．
提出问题：当x＞0时如何求函数y=x+$\frac{1}{x}$的最大值或最小值？分析问题：前面我们刚刚学过二次函数的相关知识，知道求二次函数的最值时，我们可以利用它的图象进行猜想最值，或利用配方可以求出它的最值．
例如我们求函数y=x-2$\sqrt{x}$（x＞0）的最值时，就可以仿照二次函数利用配方求最值的方法解决问题；y=x-2$\sqrt{x}$=（$\sqrt{x}$）2-2$\sqrt{x}$-2$\sqrt{x}$+1-1=（$\sqrt{x}$-1）2-1即当x=1时，y有最小值为-1
解决问题
借鉴我们已有的研究函数的经验，探索函数y=x+$\frac{1}{x}$（x＞0）的最大（小）值．
（1）实践操作：填写下表，并用描点法画出函数y=x+$\frac{1}{x}$（x＞0）的图象：
| x | … | $\frac{1}{4}$ | $\frac{1}{3}$ | $\frac{1}{2}$ | 1 | 2 | 3 | 4 | … |
| y | … | … |
当x=1时，函数y=x+$\frac{1}{x}$（x＞0）有最小值（填“大”或“小”），是2．
（3）推理论证：利用上述例题，请你尝试通过配方法求函数y=x+$\frac{1}{x}$（x＞0）的最大（小）值，以证明你的猜想．知识能力运用：直接写出函数y=-2x-$\frac{1}{2x}$（x＞0）当x=$\frac{1}{2}$时，该函数有最大值（填“大”或“小”），是-2．
如图，已知点A、B、C的坐标分别A（1，6）、B（1，0）、C（5，0）．若点P在∠ABC的平分线上，且PA=PC，则点P的坐标为（6，5）．