题目内容
2.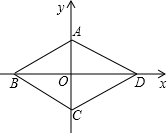 如图,在平面直角坐标系中,菱形ABCD的边长为17,点A的坐标为(0,8)求点B,C,D的坐标.
如图,在平面直角坐标系中,菱形ABCD的边长为17,点A的坐标为(0,8)求点B,C,D的坐标.
分析 根据菱形的性质得出AO=OC,OB=OD,根据勾股定理求出OD,即可得出答案.
解答 解:∵四边形ABCD是菱形,菱形ABCD的边长为17,
∴AO=OC,OB=OD,AD=AB=BC=CD=17,
∵点A的坐标为(0,8),
∴OA=8=OC,
在Rt△AOD中,由勾股定理得:OD=$\sqrt{1{7}^{2}-{8}^{2}}$=15,
即OD=OB=15,
∴B点的坐标为(-15,0),C点的坐标为(0,-8),D点的坐标为(15,0).
点评 本题考查了菱形的性质和勾股定理,能熟记菱形的性质是解此题的关键,注意:菱形的对角线互相平分,菱形的四条边都相等.

练习册系列答案
 补充习题江苏系列答案
补充习题江苏系列答案 学练快车道口算心算速算天天练系列答案
学练快车道口算心算速算天天练系列答案
相关题目
13.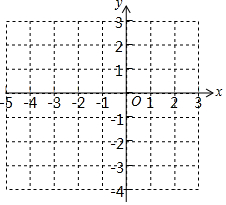 二次函数y=ax2+bx+c(a≠0)图象上部分点的横坐标x,纵坐标y的对应值
二次函数y=ax2+bx+c(a≠0)图象上部分点的横坐标x,纵坐标y的对应值
如下表:
(1)求这个二次函数的表达式;
(2)在右图中画出此二次函数的图象的示意图;
(3)结合图象,直接写出当y>0时,自变量x的取值范围.
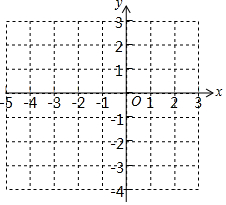 二次函数y=ax2+bx+c(a≠0)图象上部分点的横坐标x,纵坐标y的对应值
二次函数y=ax2+bx+c(a≠0)图象上部分点的横坐标x,纵坐标y的对应值如下表:
| x | … | -4 | -3 | -2 | -1 | 0 | 1 | 2 | … |
| y | … | -$\frac{5}{2}$ | 0 | $\frac{3}{2}$ | 2 | $\frac{3}{2}$ | 0 | -$\frac{5}{2}$ | … |
(2)在右图中画出此二次函数的图象的示意图;
(3)结合图象,直接写出当y>0时,自变量x的取值范围.
11.下列各命题的逆命题成立的是( )
| A. | 三个内角相等的三角形是等边三角形 | |
| B. | 对顶角相等 | |
| C. | 三角形中,钝角所对的边最长 | |
| D. | 全等三角形的对应角相等 |
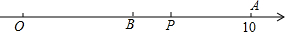 如图,数轴上的点O和A分别表示0和10,点P是线段OA上一动点,沿O→A→O以每秒2个单位的速度往返运动1次,B是线段OA的中点,设点P运动时间为t秒(0≤t≤10).
如图,数轴上的点O和A分别表示0和10,点P是线段OA上一动点,沿O→A→O以每秒2个单位的速度往返运动1次,B是线段OA的中点,设点P运动时间为t秒(0≤t≤10). 如图,AC是?ABCD的对角线,点E、F在AC上,且四边形EBFD也是平行四边形,求证:AE=CF(思考不用全等的方法)
如图,AC是?ABCD的对角线,点E、F在AC上,且四边形EBFD也是平行四边形,求证:AE=CF(思考不用全等的方法)