题目内容
15. 如图,在△ABC中,BC=2,tan∠A=$\frac{1}{2}$,求△ABC的外接圆半径.
如图,在△ABC中,BC=2,tan∠A=$\frac{1}{2}$,求△ABC的外接圆半径.
分析 过点B作直径BE,连结CE,如图,根据圆周角定理得到∠BCE=90°,∠E=∠A,则tan∠E=$\frac{1}{2}$,在Rt△BCE中理由正切的定义可计算出CE=4,则易得BE,可得结果.
解答 解:过点B作直径BE,连结CE,如图,
∵BE为直径,
∴∠BCE=90°,
∵∠E=∠A,
∴tan∠E=$\frac{1}{2}$,
在Rt△BCE中,tan∠E=$\frac{BC}{CE}$=$\frac{1}{2}$,
而BC=2,
∴CE=4,
∴BE=$\sqrt{{2}^{2}{+4}^{2}}$=2$\sqrt{5}$,
∴△ABC的外接圆的半径为$\sqrt{5}$.
点评 本题主要考查了周角定理,作出恰当的辅助线是解答此题的关键.

练习册系列答案
 开心蛙状元测试卷系列答案
开心蛙状元测试卷系列答案
相关题目
5.某市在端午节准备举行划龙舟大赛,预计15个队共330人参加.已知每个队一条船,每条船上人数相等,且每条船上有1人击鼓,1人掌舵,其余的人同时划桨.如果设每条船上划桨的有x人,那么可列出一元一次方程为( )
| A. | 15(x-2)=330 | B. | 15x+2=330 | C. | 15(x+2)=330 | D. | 15x-2=330 |
3.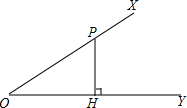 如图,P为∠XOY上一点,作PH⊥OY于H,对于sin2∠XOY+cos2∠XOY的大小,下列说法正确的是( )
如图,P为∠XOY上一点,作PH⊥OY于H,对于sin2∠XOY+cos2∠XOY的大小,下列说法正确的是( )
 如图,P为∠XOY上一点,作PH⊥OY于H,对于sin2∠XOY+cos2∠XOY的大小,下列说法正确的是( )
如图,P为∠XOY上一点,作PH⊥OY于H,对于sin2∠XOY+cos2∠XOY的大小,下列说法正确的是( )| A. | 与点P的位置有关 | B. | 与PH的长度有关 | ||
| C. | 与∠XOY的大小有关 | D. | 与点P的位置和∠XOY的大小都无关 |
4.下列方程中,在实数范围内有解的是( )
| A. | x2-x+1=0 | B. | $\sqrt{2x-1}$+2=0 | C. | $\frac{1}{x-5}=\frac{x-4}{x-5}$ | D. | $\sqrt{x-2}+\sqrt{2-x}=0$ |
