题目内容
8.已知x=$\frac{4-\sqrt{7}}{3}$,求$\frac{{x}^{2}}{{x}^{4}+{x}^{2}+1}$.分析 先运用分母有理化求出x+$\frac{1}{x}$的值,再把所求的分式根据分式的基本性质进行变形,代入计算即可.
解答 解:∵x=$\frac{4-\sqrt{7}}{3}$,
∴x+$\frac{1}{x}$=$\frac{4-\sqrt{7}}{3}$+$\frac{3}{4-\sqrt{7}}$
=$\frac{4-\sqrt{7}}{3}$+$\frac{3(4+\sqrt{7})}{{4}^{2}-7}$
=$\frac{4-\sqrt{7}}{3}$+$\frac{4+\sqrt{7}}{3}$
=$\frac{8}{3}$
原式=$\frac{1}{{x}^{2}+1+\frac{1}{{x}^{2}}}$
=$\frac{1}{{(x+\frac{1}{x})}^{2}-2+1}$
=$\frac{1}{{(\frac{8}{3})}^{2}-1}$
=$\frac{9}{55}$
点评 本题考查的是二次根式的化简求值,正确进行分母有理化和分式的变形是解题的关键.

练习册系列答案
 轻松暑假总复习系列答案
轻松暑假总复习系列答案
相关题目
18.在实数:3.14159,$\root{3}{64}$,1.010010001…(每相隔1个就多1个0),$4.\stackrel{..}{21}$,π,$\frac{22}{7}$中,无理数的个数有( )
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
16.某工程车准备将17根水泥电杆从公司拉到1千米以外的公路旁栽立,每隔0.1千米栽一根,汽车从公司出发到完成任务后返回公司称为汽车行驶的总路程,为y千米.由于汽车载重量有限,每趟最多能拉3根水泥杆,为使总路程y尽可能少,汽车除第x趟(x为不大于6的自然数)拉2根外,其余5趟均拉3根,则y与x的函数为( )
| A. | y=0.2x+18.5(1≤x≤6) | B. | y=0.2x+18.7(1≤x≤6) | ||
| C. | y=0.2x+22(1≤x≤6) | D. | y=0.2x+22.2(1≤x≤6) |
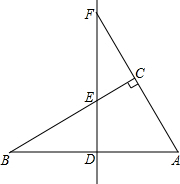 如图,在△ABC中,∠ACB=90°,AB的垂直平分线交AB于点D,交边BC于点E,交边AC的延长线于点F,并且BD=CF.求证:∠CAB=2∠B.
如图,在△ABC中,∠ACB=90°,AB的垂直平分线交AB于点D,交边BC于点E,交边AC的延长线于点F,并且BD=CF.求证:∠CAB=2∠B.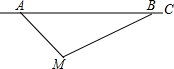 根据道路管理规定,在贺州某段笔直公路上行驶的车辆,限速40千米/时,已知交警测速点M到该公路A点的距离为10$\sqrt{2}$米,∠MAB=45°,∠MBA=30°(如图所示),现有一辆汽车由A往B方向匀速行驶,测得此车从A点行驶到B点所用的时间为3秒.
根据道路管理规定,在贺州某段笔直公路上行驶的车辆,限速40千米/时,已知交警测速点M到该公路A点的距离为10$\sqrt{2}$米,∠MAB=45°,∠MBA=30°(如图所示),现有一辆汽车由A往B方向匀速行驶,测得此车从A点行驶到B点所用的时间为3秒.