题目内容
16.某工程车准备将17根水泥电杆从公司拉到1千米以外的公路旁栽立,每隔0.1千米栽一根,汽车从公司出发到完成任务后返回公司称为汽车行驶的总路程,为y千米.由于汽车载重量有限,每趟最多能拉3根水泥杆,为使总路程y尽可能少,汽车除第x趟(x为不大于6的自然数)拉2根外,其余5趟均拉3根,则y与x的函数为( )| A. | y=0.2x+18.5(1≤x≤6) | B. | y=0.2x+18.7(1≤x≤6) | ||
| C. | y=0.2x+22(1≤x≤6) | D. | y=0.2x+22.2(1≤x≤6) |
分析 根据题意首先求出x=1时,y的值,即拉第一趟时,到一千米以外,种下第一个,再走0.1km,种下第二个,再返回,共(1+0.1)×2km,拉第二趟时,到一千米以外,走过之前种下第一、二个,再走0.1km,种下第三个,以此类推,种到第五个再返回,共(1+0.1+0.3)×2km…,拉第6趟:共(1+0.1+0.3+0.3+0.3+0.3+0.3)×2km,共(1+0.1)×2+(1+0.1+0.3)×2+(1+0.1+0.3+0.3)×2+(1+0.1+0.3+0.3+0.3)×2+(1+0.1+0.3+0.3+0.3+0.3)×2+(1+0.1+0.3+0.3+0.3+0.3+0.3)×2=22.2km,进而得出x=6时,行驶的总路程,求出函数解析式.
解答 解:根据题意可得:当x=1时,
y=(1+0.1)×2+(1+0.1+0.3)×2+(1+0.1+0.3+0.3)×2+(1+0.1+0.3+0.3+0.3)×2+(1+0.1+0.3+0.3+0.3+0.3)×2+(1+0.1+0.3+0.3+0.3+0.3+0.3)×2
=22.2(km)
当x=6时,y=(1+0.3)×2+(1+0.3+0.3)×2+(1+0.3+0.3+0.3)×2+(1+0.3+0.3+0.3+0.3)×2+(1+0.3+0.3+0.3+0.3+0.3)×2+(1+0.3+0.3+0.3+0.3+0.3+0.1)×2=23.2
设关系式为y=kx+b,由题意有:$\left\{\begin{array}{l}{22.2=k+b}\\{23.2=6k+b}\end{array}\right.$,
解得:$\left\{\begin{array}{l}{k=0.2}\\{b=22}\end{array}\right.$,则有y=0.2x+22(1≤x≤6).
故选:C.
点评 此题主要考查了根据实际问题列一次函数解析式,得出x=1和x=6时y的值是解题关键.

| A. | 没有明确调查问题 | B. | 没有规定调查方法 | ||
| C. | 没有确定对象 | D. | 没有展开调查 |
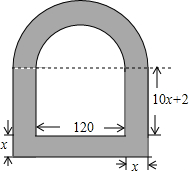 求如图所示的窗户的边框面积(上部为半圆).(单位:cm)
求如图所示的窗户的边框面积(上部为半圆).(单位:cm)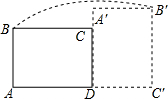 如图,在矩形ABCD中,AB=3,AD=4,将矩形ABCD绕点D顺时针旋转90°得到矩形A′B′C′D′,则点B经过的路径与BA,AC′,C′B′所围成封闭图形的面积是$\frac{25π}{4}$+12(结果保留π).
如图,在矩形ABCD中,AB=3,AD=4,将矩形ABCD绕点D顺时针旋转90°得到矩形A′B′C′D′,则点B经过的路径与BA,AC′,C′B′所围成封闭图形的面积是$\frac{25π}{4}$+12(结果保留π).