题目内容
19.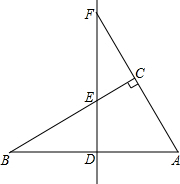 如图,在△ABC中,∠ACB=90°,AB的垂直平分线交AB于点D,交边BC于点E,交边AC的延长线于点F,并且BD=CF.求证:∠CAB=2∠B.
如图,在△ABC中,∠ACB=90°,AB的垂直平分线交AB于点D,交边BC于点E,交边AC的延长线于点F,并且BD=CF.求证:∠CAB=2∠B.
分析 连接AE,根据线段垂直平分线的性质得到BE=AE,BD=AD,通过△BDE≌△CFE,得到∠B=∠F,BE=EF,等量代换得到EF=AE,证得∠EAC=∠F,于是得到结论.
解答 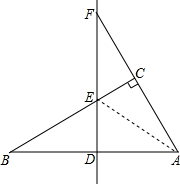 解:连接AE,∵DF垂直平分AB,
解:连接AE,∵DF垂直平分AB,
∴BE=AE,BD=AD,
∴∠EAD=∠B,
在△BDE与△CEF中$\left\{\begin{array}{l}{∠BDE=∠ECF=90°}\\{∠BED=∠FEC}\\{BD=CF}\end{array}\right.$,
∴△BDE≌△CFE,
∴∠B=∠F,BE=EF,
∴EF=AE,
∴∠EAC=∠F,
∴∠EAC=∠B,
∴∠CAB=2∠B.
点评 本题考查了线段的垂直平分线的性质,全等三角形的判定和性质,连接AE,构造全等三角形是解题的关键.

练习册系列答案
 寒假大串联黄山书社系列答案
寒假大串联黄山书社系列答案
相关题目
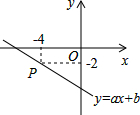 在教学活动中我们知道,任何一个二元一次方程的图象都是一条直线,如图,已知直线y=ax-6过点P(-4,-2),则关于x、y的方程组$\left\{\begin{array}{l}{y=ax-6}\\{y=\frac{1}{2}x}\end{array}\right.$的解是$\left\{\begin{array}{l}{x=-4}\\{y=-2}\end{array}\right.$.
在教学活动中我们知道,任何一个二元一次方程的图象都是一条直线,如图,已知直线y=ax-6过点P(-4,-2),则关于x、y的方程组$\left\{\begin{array}{l}{y=ax-6}\\{y=\frac{1}{2}x}\end{array}\right.$的解是$\left\{\begin{array}{l}{x=-4}\\{y=-2}\end{array}\right.$.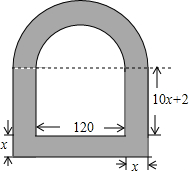 求如图所示的窗户的边框面积(上部为半圆).(单位:cm)
求如图所示的窗户的边框面积(上部为半圆).(单位:cm)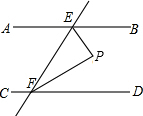 已知:如图,AB∥CD,直线EF分别交AB、CD于点E、F,∠BEF的平分线与∠DFE的平分线相交于点P,求∠P.
已知:如图,AB∥CD,直线EF分别交AB、CD于点E、F,∠BEF的平分线与∠DFE的平分线相交于点P,求∠P.