题目内容
20.解方程组:$\left\{\begin{array}{l}{3x^2-y^2=8}\\{x^2+xy+y^2=4}\end{array}\right.$.分析 根据加减消元法,可得x2-2xy-3y2=0,根据因式分解,可得x、y的关系.
解答 解:$\left\{\begin{array}{l}{3{x}^{2}-{y}^{2}=8①}\\{{x}^{2}+xy+{y}^{2}=4②}\end{array}\right.$
①-②×2,得
x2-2xy-3y2=0.
因式分解,得
(x+y)(x-3y)=0.
解得x=-y,或x=3y.
当x=-y时,x=-y=±2,$\left\{\begin{array}{l}{x=2}\\{y=-2}\end{array}\right.$或$\left\{\begin{array}{l}{x=-2}\\{y=2}\end{array}\right.$,
当x=3y时,y=$±\frac{2\sqrt{13}}{13}$,$\left\{\begin{array}{l}{x=\frac{6\sqrt{13}}{13}}\\{y=\frac{2\sqrt{13}}{13}}\end{array}\right.$或$\left\{\begin{array}{l}{x=-\frac{6\sqrt{13}}{13}}\\{y=-\frac{2\sqrt{13}}{13}}\end{array}\right.$,
原方程组的解为$\left\{\begin{array}{l}{x=2}\\{y=-2}\end{array}\right.$或$\left\{\begin{array}{l}{x=-2}\\{y=2}\end{array}\right.$,$\left\{\begin{array}{l}{x=\frac{6\sqrt{13}}{13}}\\{y=\frac{2\sqrt{13}}{13}}\end{array}\right.$或$\left\{\begin{array}{l}{x=-\frac{6\sqrt{13}}{13}}\\{y=-\frac{2\sqrt{13}}{13}}\end{array}\right.$.
点评 本题考查了高次方程,加减消元是解题常用方法,因式分解是解题关键.

 学期复习一本通学习总动员期末加暑假延边人民出版社系列答案
学期复习一本通学习总动员期末加暑假延边人民出版社系列答案 芒果教辅暑假天地重庆出版社系列答案
芒果教辅暑假天地重庆出版社系列答案| A. | $\frac{\sqrt{6}}{2}$ | B. | $\sqrt{2}$ | C. | 2-$\sqrt{2}$ | D. | $\frac{2+\sqrt{2}}{2}$ |
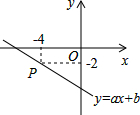 在教学活动中我们知道,任何一个二元一次方程的图象都是一条直线,如图,已知直线y=ax-6过点P(-4,-2),则关于x、y的方程组$\left\{\begin{array}{l}{y=ax-6}\\{y=\frac{1}{2}x}\end{array}\right.$的解是$\left\{\begin{array}{l}{x=-4}\\{y=-2}\end{array}\right.$.
在教学活动中我们知道,任何一个二元一次方程的图象都是一条直线,如图,已知直线y=ax-6过点P(-4,-2),则关于x、y的方程组$\left\{\begin{array}{l}{y=ax-6}\\{y=\frac{1}{2}x}\end{array}\right.$的解是$\left\{\begin{array}{l}{x=-4}\\{y=-2}\end{array}\right.$.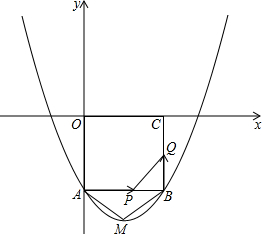 如图,在平面直角坐标系xOy中,正方形OABC的边长为2cm,点A、C分别在y轴的负半轴和x轴的正半轴上,抛物线y=ax2+bx+c经过点A、B,最低点为M,且S△AMB=$\frac{5}{6}$
如图,在平面直角坐标系xOy中,正方形OABC的边长为2cm,点A、C分别在y轴的负半轴和x轴的正半轴上,抛物线y=ax2+bx+c经过点A、B,最低点为M,且S△AMB=$\frac{5}{6}$