题目内容
12.已知x+y=4,xy=2,求$\frac{y+1}{x+1}$+$\frac{x+1}{y+1}$的值.分析 根据x+y=4,xy=2,得出x2+y2=(x+y)2-2xy=12,再把要求的式子进行通分,然后代值计算即可.
解答 解:∵x+y=4,xy=2,
∴x2+y2=(x+y)2-2xy=42-4=12,
∴$\frac{y+1}{x+1}$+$\frac{x+1}{y+1}$=$\frac{(y+1)^{2}}{(x+1)(y+1)}$+$\frac{(x+1)^{2}}{(x+1)(y+1)}$=$\frac{{x}^{2}+{y}^{2}+2(x+y)+2}{xy+x+y+1}$=$\frac{12-2×4+2}{2+4+1}$=$\frac{6}{7}$.
点评 此题考查了分式的化简求值,用到的知识点是完全平方和平方差公式,关键是根据给出的条件求出x2+y2的值.

练习册系列答案
相关题目
2.观察一列单项式:2x3,-4x3,8x3,-16x3,32x3,-64x3,…则第2014个单项式是( )
| A. | -22014x3 | B. | 22014x3 | C. | -24018x3 | D. | 24018x3 |
3.在平面内,下列数据不能确定物体位置的是( )
| A. | 电影票“3排5座” | B. | 北偏西40° | ||
| C. | 北京路20号 | D. | 东经120°,北纬30° |
4. 如图,已知∠1与∠2互补,∠3=100°,那么∠4的度数为( )
如图,已知∠1与∠2互补,∠3=100°,那么∠4的度数为( )
 如图,已知∠1与∠2互补,∠3=100°,那么∠4的度数为( )
如图,已知∠1与∠2互补,∠3=100°,那么∠4的度数为( )| A. | 70° | B. | 75° | C. | 80° | D. | 85° |
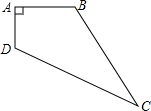 如图,一块四边形的土地,其中∠DAB=90°,AB=4m,AD=3m,BC=12m,CD=13m,则这块土地的面积是36m2.
如图,一块四边形的土地,其中∠DAB=90°,AB=4m,AD=3m,BC=12m,CD=13m,则这块土地的面积是36m2.