题目内容
在平面直角坐标系 中,已知一次函数
中,已知一次函数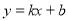 的图像经过点P(1,1),与
的图像经过点P(1,1),与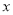 轴交于点A,与
轴交于点A,与 轴交于点B,且
轴交于点B,且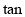 ∠ABO=3,那么A点的坐标是 .
∠ABO=3,那么A点的坐标是 .
(-2,0)或(4,0).
【解析】
试题分析:已知tan∠ABO=3就是已知一次函数的一次项系数是 或-
或- .根据函数经过点P,利用待定系数法即可求得函数解析式,进而可得到A的坐标.
.根据函数经过点P,利用待定系数法即可求得函数解析式,进而可得到A的坐标.
试题解析:在Rt△AOB中,由tan∠ABO=3,可得OA=3OB,则一次函数y=kx+b中k=± .
.

∵一次函数y=kx+b(k≠0)的图象过点P(1,1),
∴当k= 时,求可得b=
时,求可得b= ;
;
k=- 时,求可得b=
时,求可得b= .
.
即一次函数的解析式为y= x+
x+ 或y=-
或y=- x+
x+ .
.
令y=0,则x=-2或4,
∴点A的坐标是(-2,0)或(4,0).
考点:1.待定系数法求一次函数解析式;2.锐角三角函数的定义.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
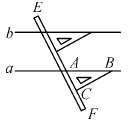
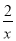 (x>0)的图象上,过点B1分别作x轴和y轴的垂线,垂足为C1和A,得到第一个矩形AOC1B1,点C1的坐标为(1,0);取x轴上一点C2(
(x>0)的图象上,过点B1分别作x轴和y轴的垂线,垂足为C1和A,得到第一个矩形AOC1B1,点C1的坐标为(1,0);取x轴上一点C2( ,0),过点C2作x轴的垂线交反比例函数图象于点B2,过B2作线段B2 A1⊥B1C1,,交B1C1于点A1,得到第二个矩形A1C1C2B2;依次在x轴上取点C3(2,0),C4(
,0),过点C2作x轴的垂线交反比例函数图象于点B2,过B2作线段B2 A1⊥B1C1,,交B1C1于点A1,得到第二个矩形A1C1C2B2;依次在x轴上取点C3(2,0),C4(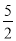 ,0) 按此规律作矩形,则第10个矩形A9C9C10B10的面积为 .
,0) 按此规律作矩形,则第10个矩形A9C9C10B10的面积为 .


 与
与 轴只有一个交点,则b的值为____________。
轴只有一个交点,则b的值为____________。