题目内容
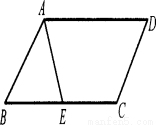
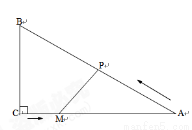
已知:如图,菱形ABCD中,对角线AC,BD相交于点O,且AC=12cm,BD=16cm.点P从点B出发,沿BA方向匀速运动,速度为1cm/s;同时,直线EF从点D出发,沿DB方向匀速运动,速度为1cm/s,EF⊥BD,且与AD,BD,CD分别交于点E,Q,F;当直线EF停止运动时,点P也停止运动.连接PF,设运动时间为t(s)(0<t<8).解答下列问题:
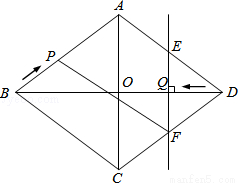
(1)当t为何值时,四边形APFD是平行四边形?
(2)设四边形APFE的面积为y(cm2),求y与t之间的函数关系式;
(3)是否存在某一时刻t,使S四边形APFE:S菱形ABCD=17:40?若存在,求出t的值,并求出此时P,E两点间的距离;若不存在,请说明理由.
(1) 当t=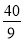 s时,四边形APFD是平行四边形.(2)y=-
s时,四边形APFD是平行四边形.(2)y=-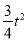 +
+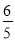 t+48.(3)
t+48.(3) 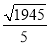 cm.
cm.
【解析】
试题分析:(1))由四边形ABCD是菱形,OA=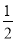 AC,OB=
AC,OB=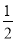 BD.在Rt△AOB中,运用勾股定理求出AB=10.再由△DFQ∽△DCO.得出
BD.在Rt△AOB中,运用勾股定理求出AB=10.再由△DFQ∽△DCO.得出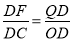 .求出DF.由AP=DF.求出t.
.求出DF.由AP=DF.求出t.
(2)过点C作CG⊥AB于点G,由S菱形ABCD=ABCG=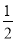 ACBD,求出CG.据S梯形APFD=
ACBD,求出CG.据S梯形APFD=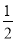 (AP+DF)CG.S△EFD=
(AP+DF)CG.S△EFD=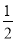 EFQD.得出y与t之间的函数关系式;
EFQD.得出y与t之间的函数关系式;
(3)过点C作CG⊥AB于点G,由S菱形ABCD=ABCG,求出CG,由S四边形APFE:S菱形ABCD=17:40,求出t,再由△PBN∽△ABO,求得PN,BN,据线段关系求出EM,PM再由勾股定理求出PE.
试题解析:(1)∵四边形ABCD是菱形,
∴AB∥CD,AC⊥BD,OA=OC=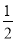 AC=6, OB=OD=
AC=6, OB=OD=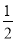 BD=8.
BD=8.
在Rt△AOB中,AB=10
∵EF⊥BD,
∴∠FQD=∠COD=90°.
又∵∠FDQ=∠CDO,
∴△DFQ∽△DCO.
∴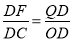 .即
.即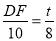
∴DF=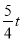
∵四边形APFD是平行四边形,
∴AP=DF.
即10-t=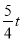
解这个方程,得t=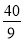 .
.
∴当t=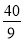 s时,四边形APFD是平行四边形.
s时,四边形APFD是平行四边形.
(2)如图,过点C作CG⊥AB于点G,
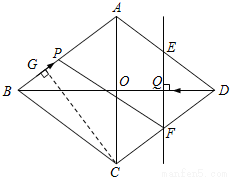
∵S菱形ABCD=ABCG=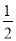 ACBD,
ACBD,
即10CG=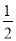 ×12×16,
×12×16,
∴CG=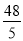
∴S梯形APFD=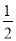 (AP+DF)CG
(AP+DF)CG
=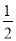 (10-t+
(10-t+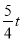 )
)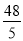
=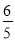 t+48.
t+48.
∵△DFQ∽△DCO,
∴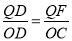
即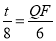
∴QF=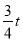 .
.
同理,EQ=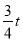
∴EF=QF+EQ=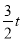 .
.
∴S△EFD=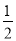 EFQD=
EFQD=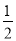 ×
×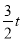 ×t=
×t=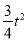 .
.
∴y=(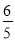 t+48)-
t+48)-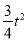 =-
=-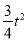 +
+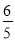 t+48.
t+48.
(3)如图,过点P作PM⊥EF于点M,PN⊥BD于点N,
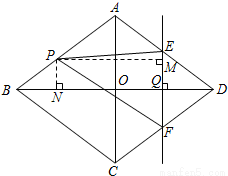
若S四边形APFE:S菱形ABCD=17:40,
则-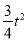 +
+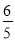 t+48=
t+48=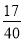 ×96,
×96,
即5t2-8t-48=0,
解这个方程,得t1=4,t2=-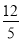 (舍去)
(舍去)
过点P作PM⊥EF于点M,PN⊥BD于点N,
当t=4时,
∵△PBN∽△ABO,
∴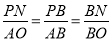
即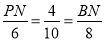
∴PN=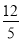 ,BN=
,BN=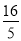
∴EM=EQ-MQ=3-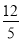 =
=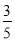
PM=BD-BN-DQ=16-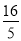 -4=
-4=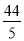
在Rt△PME中,
PE=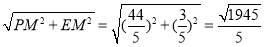 cm.
cm.
考点:1.四边形综合题;2.相似三角形的性质.

 (cm),求y与t之间的函数关系式;
(cm),求y与t之间的函数关系式; ?若存在,求出相应t的值,若不存在,说明理由;
?若存在,求出相应t的值,若不存在,说明理由; ,则袋中红球约为 _____个.
,则袋中红球约为 _____个.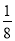 B.
B.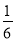 C.
C.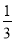 D.
D.
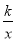 的图象相交于A,B两点,与x轴相交于点C.已知tan∠BOC=
的图象相交于A,B两点,与x轴相交于点C.已知tan∠BOC=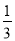 ,点B的坐标为(m,n).
,点B的坐标为(m,n).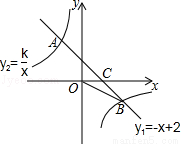
 中,已知一次函数
中,已知一次函数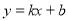 的图像经过点P(1,1),与
的图像经过点P(1,1),与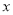 轴交于点A,与
轴交于点A,与 轴交于点B,且
轴交于点B,且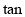 ∠ABO=3,那么A点的坐标是 .
∠ABO=3,那么A点的坐标是 .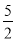 C.2 D.
C.2 D.