题目内容
20.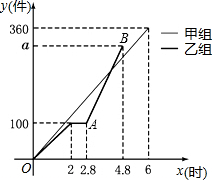 甲、乙两组工人同时加工某种零件,乙组工作中有一次停产更换设备,更换设备后,乙组的工作效率是原来的2倍.两组各自加工零件的数量y(件)与时间x(时)的函数图象如图所示.下列说法:①甲组加工零件的总量比乙组加工零件总量多;②乙组加工零件总量的a值是300件;③甲、乙两组加工出的零件合在一起装箱,每够300件装一箱,零件装箱的时间忽略不计,经过3小时恰好装满第1箱④经过4.5小时甲、乙两组加工出的零件数相同,其中正确的个数为( )
甲、乙两组工人同时加工某种零件,乙组工作中有一次停产更换设备,更换设备后,乙组的工作效率是原来的2倍.两组各自加工零件的数量y(件)与时间x(时)的函数图象如图所示.下列说法:①甲组加工零件的总量比乙组加工零件总量多;②乙组加工零件总量的a值是300件;③甲、乙两组加工出的零件合在一起装箱,每够300件装一箱,零件装箱的时间忽略不计,经过3小时恰好装满第1箱④经过4.5小时甲、乙两组加工出的零件数相同,其中正确的个数为( )| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
分析 根据函数的图象进行分析,再利用乙的原来加工速度得出更换设备后,乙组的工作速度进行解答即可.
解答 解:①由图象可得甲组加工零件的总量比乙组加工零件总量多,正确;②乙2小时加工100件,
∴乙的加工速度是:每小时50件,
∴乙组在工作中有一次停产更换设备,更换设备后,乙组的工作效率是原来的2倍.
∴更换设备后,乙组的工作速度是:每小时加工50×2=100件,
a=100+100×(4.8-2.8)=300,
乙组加工零件总量的a值是300件,正确;③乙组更换设备后,乙组加工的零件的个数y与时间x的函数关系式为:
y=100+100(x-2.8)=100x-180,
当0≤x≤2时,60x+50x=300,解得:x=$\frac{30}{11}$(不合题意舍去);
当2<x≤2.8时,100+60x=300,解得:x=$\frac{10}{3}$(不合题意舍去);
∵当2.8<x≤4.8时,60x+100x-180=300,
解得x=3,
∴经过3小时恰好装满第1箱,
甲、乙两组加工出的零件合在一起装箱,每够300件装一箱,零件装箱的时间忽略不计,经过3小时恰好装满第1箱,正确;
④经过4.5小时甲、乙两组加工出的零件数相同,正确;
故选D
点评 此题主要考查了一次函数的应用,根据题意得出函数关系式以及数形结合是解决问题的关键.

练习册系列答案
相关题目
10.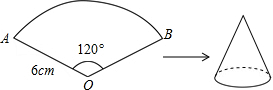 如图已知扇形AOB的半径为6cm,圆心角的度数为120°,若将此扇形围成一个圆锥的侧面,则围成的圆锥的底面积为( )
如图已知扇形AOB的半径为6cm,圆心角的度数为120°,若将此扇形围成一个圆锥的侧面,则围成的圆锥的底面积为( )
 如图已知扇形AOB的半径为6cm,圆心角的度数为120°,若将此扇形围成一个圆锥的侧面,则围成的圆锥的底面积为( )
如图已知扇形AOB的半径为6cm,圆心角的度数为120°,若将此扇形围成一个圆锥的侧面,则围成的圆锥的底面积为( )| A. | 4πcm2 | B. | 6πcm2 | C. | 9πcm2 | D. | 12πcm2 |
11.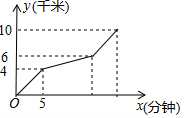 如图,小磊老师从甲地去往10千米的乙地,开始以一定的速度行驶,之后由于道路维修,速度变为原来的四分之一,过了维修道路后又变为原来的速度到达乙地.设小磊老师行驶的时间为x(分钟),行驶的路程为y(千米),图中的折线表示y与x之间的函数关系,则小磊老师从甲地到达乙地所用的时间是( )
如图,小磊老师从甲地去往10千米的乙地,开始以一定的速度行驶,之后由于道路维修,速度变为原来的四分之一,过了维修道路后又变为原来的速度到达乙地.设小磊老师行驶的时间为x(分钟),行驶的路程为y(千米),图中的折线表示y与x之间的函数关系,则小磊老师从甲地到达乙地所用的时间是( )
 如图,小磊老师从甲地去往10千米的乙地,开始以一定的速度行驶,之后由于道路维修,速度变为原来的四分之一,过了维修道路后又变为原来的速度到达乙地.设小磊老师行驶的时间为x(分钟),行驶的路程为y(千米),图中的折线表示y与x之间的函数关系,则小磊老师从甲地到达乙地所用的时间是( )
如图,小磊老师从甲地去往10千米的乙地,开始以一定的速度行驶,之后由于道路维修,速度变为原来的四分之一,过了维修道路后又变为原来的速度到达乙地.设小磊老师行驶的时间为x(分钟),行驶的路程为y(千米),图中的折线表示y与x之间的函数关系,则小磊老师从甲地到达乙地所用的时间是( )| A. | 15分钟 | B. | 20分钟 | C. | 25分钟 | D. | 30分钟 |
2.铁一课间餐种类繁多,深受学生喜爱.这天饭堂在课间的出品有鸡腿、薯饼、鱼丸和鸡柳.某同学就九年级学生对课间餐各类食物的喜爱程度做了抽样调查,制成表格如下:
(1)样本容量是250,a=12%,b=30,c=16%.
(2)若小王和小李商议着一起去买课间餐,若他们对以上四种口味的课间餐喜爱程度相同.请你帮他们算一算他们买了相同课间餐的概率.
| 课间餐种类 | 人类 | 百分比 |
| 鸡腿 | 150 | 60% |
| 薯饼 | 30 | a |
| 鱼丸 | b | 12% |
| 鸡柳 | 40 | c |
(2)若小王和小李商议着一起去买课间餐,若他们对以上四种口味的课间餐喜爱程度相同.请你帮他们算一算他们买了相同课间餐的概率.
 如图,在5×5正方形网格中,一条圆弧经过A,B,C三点.
如图,在5×5正方形网格中,一条圆弧经过A,B,C三点. 已知,A市到B市的路程为260千米,甲车从A市前往B市运送物资,行驶2小时在M地汽车出现故障,立即通知技术人员乘乙车从A市赶来维修(通知时间忽略不计),乙车到达M地后又经过20分钟修好甲车后以原速原路返回A市,同时甲车以原来1.5倍的速度前往B市,如图是两车距A市的路程y(千米)与甲车所用时间x(小时)之间的函数图象,下列四种说法:
已知,A市到B市的路程为260千米,甲车从A市前往B市运送物资,行驶2小时在M地汽车出现故障,立即通知技术人员乘乙车从A市赶来维修(通知时间忽略不计),乙车到达M地后又经过20分钟修好甲车后以原速原路返回A市,同时甲车以原来1.5倍的速度前往B市,如图是两车距A市的路程y(千米)与甲车所用时间x(小时)之间的函数图象,下列四种说法: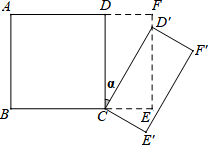 如图所示,将一个边长为2的正方形ABCD和一个长为2、宽为1的长方形CEFD拼在一起,构成一个大的长方形ABEF.现将小长方形CEFD绕点C顺时针旋转至CE′F′D′,旋转角为α.当点D′恰好落在EF边上时,旋转角α的值为30°.
如图所示,将一个边长为2的正方形ABCD和一个长为2、宽为1的长方形CEFD拼在一起,构成一个大的长方形ABEF.现将小长方形CEFD绕点C顺时针旋转至CE′F′D′,旋转角为α.当点D′恰好落在EF边上时,旋转角α的值为30°.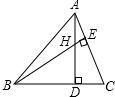 如图,在△ABC中,H是高AD和BE的交点,AD=BD,求证:DH=DC.
如图,在△ABC中,H是高AD和BE的交点,AD=BD,求证:DH=DC.