题目内容
 如图,AD∥BC,AB∥EG,AG∥BF.求证:GD=DC.
如图,AD∥BC,AB∥EG,AG∥BF.求证:GD=DC.考点:平行四边形的判定与性质,三角形中位线定理
专题:证明题
分析:由条件可证明四边ABEF和四边形ABFG为平行四边形可得EF=AB=GF,可证得F为GE的中点,由三角形中位线定理的逆定理,可知D为GC中点,可得GD=DC.
解答:证明:
∵AD∥BC,
AB∥EG,
∴四边形ABEF为平行四边形,
同理可得四边形ABFG为平行四边形,
∴EF=AB=GF,
∵AD∥BC,
∴GD=DC.
∵AD∥BC,
AB∥EG,
∴四边形ABEF为平行四边形,
同理可得四边形ABFG为平行四边形,
∴EF=AB=GF,
∵AD∥BC,
∴GD=DC.
点评:本题主要考查平行四边形的判定和性质,掌握平行四边形的判定和性质是解题的关键,即①两组对边分别平行的四边形?平行四边形,②两组对边分别相等的四边形?平行四边形,③一组对边分别平行且相等的四边形?平行四边形,④两组对角分别相等的四边形?平行四边形,⑤对角线互相平分的四边形?平行四边形.

练习册系列答案
相关题目
菱形的周长为100cm,一条对角线长为14cm,它的面积是( )
| A、168cm2 |
| B、336cm2 |
| C、672cm2 |
| D、84cm2 |
墨墨发现从某多边形的一个顶点出发,可以作4条对角线,则这个多边形的内角和是( )
| A、1260° | B、1080° |
| C、900° | D、720° |
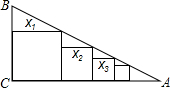 如图,在Rt△ABC中,∠C=90°,BC=a,AC=b,在△ABC中依次放入边长为x1,x2,x3,…,xn的正方形,试用a、b表示这些正方形的边长.
如图,在Rt△ABC中,∠C=90°,BC=a,AC=b,在△ABC中依次放入边长为x1,x2,x3,…,xn的正方形,试用a、b表示这些正方形的边长. 一个正方形ABCD的相邻边分别为x轴,y轴平行,且面积为9,A(1,2),试结合图形求顶点C的坐标.
一个正方形ABCD的相邻边分别为x轴,y轴平行,且面积为9,A(1,2),试结合图形求顶点C的坐标. 如图,四边形ABCD中,AB=AD,AD∥BC,∠ABC=60°,∠BCD=30°,若BC=6,试求△ACD的面积.
如图,四边形ABCD中,AB=AD,AD∥BC,∠ABC=60°,∠BCD=30°,若BC=6,试求△ACD的面积.
 在平面直角坐标系xOy中,抛物线y=x2-(m+n)x+mn(m>n)与x轴相交于A、B两点(点A位于点B的右侧),与y轴相交于点C,若m=2,n=1,求A、B两点的坐标.
在平面直角坐标系xOy中,抛物线y=x2-(m+n)x+mn(m>n)与x轴相交于A、B两点(点A位于点B的右侧),与y轴相交于点C,若m=2,n=1,求A、B两点的坐标.