题目内容
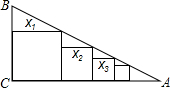如图，在Rt△ABC中，∠C=90°，BC=a，AC=b，在△ABC中依次放入边长为x1，x2，x3，…，xn的正方形，试用a、b表示这些正方形的边长．考点：相似三角形的判定与性质,正方形的性质
专题：
分析：如图，证明△ADE∽△ABC，得到
=
，解得：x1=
；运用类比的方法，同理可求x2，x3，…xn，即可解决问题．
| AE |
| AC |
| DE |
| BC |
| ab |
| a+b |
解答：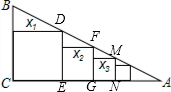
解：如图，由题意得：DE=X1，AE=b-X1；
∵DE∥BC，
∴△ADE∽△ABC，且BC=a，
∴
=
，解得：x1=
；
同理可求：X2=
，
X3=
，…Xn=
．
解：如图，由题意得：DE=X1，AE=b-X1；∵DE∥BC，
∴△ADE∽△ABC，且BC=a，
∴
| AE |
| AC |
| DE |
| BC |
| ab |
| a+b |
同理可求：X2=
| ab2 |
| (a+b)2 |
X3=
| ab3 |
| (a+b)3 |
| abn |
| (a+b)n |
点评：该题主要考查了正方形的性质、相似三角形的判定及其性质等几何知识点及其应用问题；应牢固掌握正方形的性质、相似三角形的判定及其性质；这是灵活解题的基础和关键．
练习册系列答案
相关题目
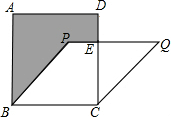如图所示，正方形ABCD与菱形PQCD的面积分别为25cm2和20cm2，阴影部分的面积为
如图，AD∥BC，AB∥EG，AG∥BF．求证：GD=DC．