题目内容
 在平面直角坐标系xOy中,抛物线y=x2-(m+n)x+mn(m>n)与x轴相交于A、B两点(点A位于点B的右侧),与y轴相交于点C,若m=2,n=1,求A、B两点的坐标.
在平面直角坐标系xOy中,抛物线y=x2-(m+n)x+mn(m>n)与x轴相交于A、B两点(点A位于点B的右侧),与y轴相交于点C,若m=2,n=1,求A、B两点的坐标.考点:抛物线与x轴的交点
专题:
分析:先求出抛物线的表达式,再令x2-3x+2=0,解得x1=1,x2=2,即可得出点A,B的坐标.
解答:解:∵抛物线y=x2-(m+n)x+mn(m>n)与x轴相交于A、B两点(点A位于点B的右侧),m=2,n=1,
∴抛物线y=x2-3x+2,
令x2-3x+2=0,解得x1=1,x2=2,
∴A(2,0),B(1,0).
∴抛物线y=x2-3x+2,
令x2-3x+2=0,解得x1=1,x2=2,
∴A(2,0),B(1,0).
点评:本题主要考查了抛物线与x轴的交点,解题的关键是得出抛物线的表达式.

练习册系列答案
相关题目
已知∠A与∠B互余,若∠A=50°,则∠B的度数是( )
| A、40° | B、50° |
| C、130° | D、140° |
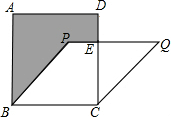 如图所示,正方形ABCD与菱形PQCD的面积分别为25cm2和20cm2,阴影部分的面积为
如图所示,正方形ABCD与菱形PQCD的面积分别为25cm2和20cm2,阴影部分的面积为 如图,AD∥BC,AB∥EG,AG∥BF.求证:GD=DC.
如图,AD∥BC,AB∥EG,AG∥BF.求证:GD=DC.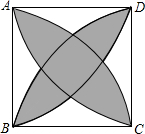 如图,正方形边长为10厘米.求阴影部分面积.
如图,正方形边长为10厘米.求阴影部分面积. 如图,已知A(-4,a),B(-1,2)是一次函数y1=kx+b与反比例函数y2=
如图,已知A(-4,a),B(-1,2)是一次函数y1=kx+b与反比例函数y2=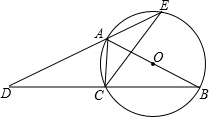 如图,AB为⊙O的直径,点C在⊙O上,延长BC至点D,使DC=BC.延长DA与⊙O的另一个交点为E,连接AC、CE.
如图,AB为⊙O的直径,点C在⊙O上,延长BC至点D,使DC=BC.延长DA与⊙O的另一个交点为E,连接AC、CE. 如图,在线段AB,BC,AC两两所夹的角中,同旁内角共有几对?把它们列举出来.
如图,在线段AB,BC,AC两两所夹的角中,同旁内角共有几对?把它们列举出来. 如图,若∠1=∠D,BD平分∠ABC,且∠ABC=55°,试求∠BCD的度数.
如图,若∠1=∠D,BD平分∠ABC,且∠ABC=55°,试求∠BCD的度数.