题目内容
 如图,四边形ABCD中,AB=AD,AD∥BC,∠ABC=60°,∠BCD=30°,若BC=6,试求△ACD的面积.
如图,四边形ABCD中,AB=AD,AD∥BC,∠ABC=60°,∠BCD=30°,若BC=6,试求△ACD的面积.考点:勾股定理
专题:
分析:过点A作AE⊥BC于E,过点D作DF⊥BC于F.构建矩形AEFD和直角三角形,通过含30度角的直角三角形的性质求得AE的长度,然后由三角形的面积公式进行解答即可.
解答: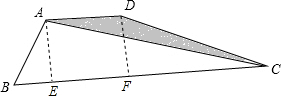 解:如图,过点A作AE⊥BC于E,过点D作DF⊥BC于F.设AB=AD=x.
解:如图,过点A作AE⊥BC于E,过点D作DF⊥BC于F.设AB=AD=x.
又∵AD∥BC,
∴四边形AEFD是矩形形,
∴AD=EF=x.
在Rt△ABE中,∠ABC=60°,则∠BAE=30°,
∴BE=
AB=
x,
∴DF=AE=
=
x,
在Rt△CDF中,∠FCD=30°,则CF=DF•cot30°=
x.
又∵BC=6,
∴BE+EF+CF=6,即
x+x+
x=6,解得x=2
∴S△ACD=
AD•DF=
x×
x=
×22=
.
 解:如图,过点A作AE⊥BC于E,过点D作DF⊥BC于F.设AB=AD=x.
解:如图,过点A作AE⊥BC于E,过点D作DF⊥BC于F.设AB=AD=x.又∵AD∥BC,
∴四边形AEFD是矩形形,
∴AD=EF=x.
在Rt△ABE中,∠ABC=60°,则∠BAE=30°,
∴BE=
| 1 |
| 2 |
| 1 |
| 2 |
∴DF=AE=
| AB2-BE2 |
| ||
| 2 |
在Rt△CDF中,∠FCD=30°,则CF=DF•cot30°=
| 3 |
| 2 |
又∵BC=6,
∴BE+EF+CF=6,即
| 1 |
| 2 |
| 3 |
| 2 |
∴S△ACD=
| 1 |
| 2 |
| 1 |
| 2 |
| ||
| 2 |
| ||
| 4 |
| 3 |
点评:本题考查的是勾股定理,熟知在任何一个直角三角形中,两条直角边长的平方之和一定等于斜边长的平方是解答此题的关键.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
如果x2+ax+1是一个完全平方式,那么a的值是( )
| A、2 | B、-2 | C、±2 | D、±1 |
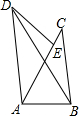 如图所示,在△ABC中,∠BAC=45°,将△ABC绕点A逆时针旋转后,能与△AED重合,已知AB=3,AC=4,则BD的长度为( )
如图所示,在△ABC中,∠BAC=45°,将△ABC绕点A逆时针旋转后,能与△AED重合,已知AB=3,AC=4,则BD的长度为( ) 如图,AD∥BC,AB∥EG,AG∥BF.求证:GD=DC.
如图,AD∥BC,AB∥EG,AG∥BF.求证:GD=DC. 如图,图中标有五条线段的长度和两个直角,求△ABC(阴影部分)的面积.
如图,图中标有五条线段的长度和两个直角,求△ABC(阴影部分)的面积. 如图,已知A(-4,a),B(-1,2)是一次函数y1=kx+b与反比例函数y2=
如图,已知A(-4,a),B(-1,2)是一次函数y1=kx+b与反比例函数y2= 已知实数a,b在数轴上的位置如图所示,则化简|a+b|+
已知实数a,b在数轴上的位置如图所示,则化简|a+b|+