题目内容
12. 如图,矩形纸片ABCD沿EF折叠后,∠FEC=25°,则∠DFD1的度数为( )
如图,矩形纸片ABCD沿EF折叠后,∠FEC=25°,则∠DFD1的度数为( )| A. | 25° | B. | 50° | C. | 75° | D. | 不能确定 |
分析 先根据平行线的性质求出∠EFG与∠EFD的度数,再由翻折变换的性质求出∠GFD1的度数,进而可得出结论.
解答 解:∵AD∥BC,∠FEC=25°,
∴∠EFG=∠FEC=25°,
∵∠EFG+∠EFD=180°,
∴∠EFD=180°-25°=155°.
由翻折变换的性质可知∠EFD1=∠EFD=155°,
∴∠GFD1=∠EFD1-∠EFG=155°-25°=130°.
∵∠DFD1+∠GFD1=180°,
∴∠DFD1=180°-130°=50°.
故选B.
点评 本题考查了平行线的性质以及角的计算,解题的关键是根据角平行线的性质找到相等的角.本题属于基础题,难度不大,解决该题型题目时,根据平行线的性质找到相等(或互补)的角是关键.

练习册系列答案
相关题目
3.下列关于x的方程以定是一元一次方程的是( )
| A. | $\frac{2}{x}$-x=1 | B. | (a2+1)x+b=0 | C. | ax2=b | D. | $\sqrt{2x+1}=5$ |
 如图,以四边形ABCD各个顶点为圆心,1cm长为半径画弧,则图中阴影部分面积之和是π cm2(结果保留π).
如图,以四边形ABCD各个顶点为圆心,1cm长为半径画弧,则图中阴影部分面积之和是π cm2(结果保留π).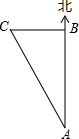 一艘在海上朝正北方向肮行的轮船,从点A到点B航行了240海里时方位仪坏了,凭经验,船长指挥船左转一定角度后,继续航行70海里后到达点C,此时AC之间的距离为250海里,你能判断船转弯后,是否沿正西方向航行?
一艘在海上朝正北方向肮行的轮船,从点A到点B航行了240海里时方位仪坏了,凭经验,船长指挥船左转一定角度后,继续航行70海里后到达点C,此时AC之间的距离为250海里,你能判断船转弯后,是否沿正西方向航行?