题目内容
20.计算:$\frac{1}{2}\sqrt{12}+|{1-\sqrt{3}}|+{(-\frac{1}{2015})^0}-2sin60°$.分析 原式第一项化为最简二次根式,第二项利用绝对值的代数意义化简,第三项利用零指数幂法则计算,最后一项利用特殊角的三角函数值计算即可得到结果.
解答 解:原式=$\frac{1}{2}$×2$\sqrt{3}$+$\sqrt{3}$-1+1-2×$\frac{\sqrt{3}}{2}$
=$\sqrt{3}$.
点评 此题考查了实数的运算,熟练掌握运算法则是解本题的关键.

练习册系列答案
相关题目
12.在△ABC中,∠C=90°,∠A=60°,AC=1,D在BC上,E在AB上,使得△ADE为等腰直角三角形,∠ADE=90°,则BE的长为( )
| A. | $4-2\sqrt{3}$ | B. | $2-\sqrt{3}$ | C. | $\sqrt{3}-1$ | D. | $\frac{1}{2}(\sqrt{3}-1)$ |
12.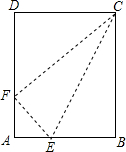 如图,小明将一块矩形纸片ABCD沿CE折叠,B点恰好落在AD边上,设此点为F,若AB:BC=3:5,则sin∠EFA的值是( )
如图,小明将一块矩形纸片ABCD沿CE折叠,B点恰好落在AD边上,设此点为F,若AB:BC=3:5,则sin∠EFA的值是( )
 如图,小明将一块矩形纸片ABCD沿CE折叠,B点恰好落在AD边上,设此点为F,若AB:BC=3:5,则sin∠EFA的值是( )
如图,小明将一块矩形纸片ABCD沿CE折叠,B点恰好落在AD边上,设此点为F,若AB:BC=3:5,则sin∠EFA的值是( )| A. | $\frac{3}{4}$ | B. | $\frac{4}{3}$ | C. | $\frac{3}{5}$ | D. | $\frac{4}{5}$ |
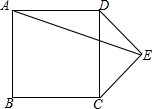 如图,在正方形ABCD外作等腰直角△CDE,DE=CE,连接AE,则sin∠AED=$\frac{\sqrt{5}}{5}$.
如图,在正方形ABCD外作等腰直角△CDE,DE=CE,连接AE,则sin∠AED=$\frac{\sqrt{5}}{5}$. 学校体育运动会的颁奖台放置于校体育馆内,其主视图如图所示,则其左视图是( )
学校体育运动会的颁奖台放置于校体育馆内,其主视图如图所示,则其左视图是( )



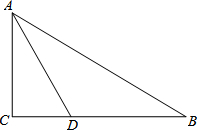 如图,在Rt△ABC中,∠C=90°,∠BAC的角平分线AD交BC于D.
如图,在Rt△ABC中,∠C=90°,∠BAC的角平分线AD交BC于D. 如图,在正方形ABCD中,AB=3cm,动点M自A点出发沿AB方向以每秒1cm的速度向B点运动,同时动点N自A点出发沿折线AD-DC-CB以每秒3cm的速度运动,到达B点时运动同时停止.设△AMN的面积为y(cm2),运动时间为x(秒),则下列图象中能大致反映y与x之间的函数关系的是( )
如图,在正方形ABCD中,AB=3cm,动点M自A点出发沿AB方向以每秒1cm的速度向B点运动,同时动点N自A点出发沿折线AD-DC-CB以每秒3cm的速度运动,到达B点时运动同时停止.设△AMN的面积为y(cm2),运动时间为x(秒),则下列图象中能大致反映y与x之间的函数关系的是( )


