题目内容
3.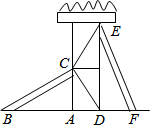 如图所示,有两个长度相同的滑梯BC和EF,CA⊥BF,ED⊥BF,垂足分别为A,D,左边滑梯的高度AC与右边滑梯水平方向的长度DF相等.问:两个滑梯的倾斜角∠ABC和∠DFE的大小有什么关系?
如图所示,有两个长度相同的滑梯BC和EF,CA⊥BF,ED⊥BF,垂足分别为A,D,左边滑梯的高度AC与右边滑梯水平方向的长度DF相等.问:两个滑梯的倾斜角∠ABC和∠DFE的大小有什么关系?
分析 由图可得,△ABC与△DEF均是直角三角形,由已知可根据HL判定两三角形全等,再根据全等三角形的对应角相等,不难求解.
解答 解:∠ABC+∠DFE=90°,理由如下:
由题意可得:△ABC与△DEF均是直角三角形,且BC=EF,AC=DF.
在Rt△ABC和Rt△DEF中,
$\left\{\begin{array}{l}{BC=EF}\\{AC=DF}\end{array}\right.$,
∴Rt△ABC≌Rt△DEF(HL),
∴∠ABC=∠DEF,
∵∠DEF+∠DFE=90°,
∴∠ABC+∠DFE=90°.
点评 此题考查了全等三角形的应用.做题时要注意找已知条件,根据已知选择方法得出全等三角形是解题关键.

练习册系列答案
相关题目
1.下列是一元二次方程的为( )
| A. | x2-4y+5=0 | B. | x2=0 | C. | ax2+bx+c=0 | D. | x2-$\frac{1}{x}$=2 |
2.若$\sqrt{x+3}$+(y-2)2=0,则(x+y)2017等于( )
| A. | -1 | B. | 1 | C. | 52017 | D. | -52017 |
19.下列方程的变形中,正确的是( )
| A. | 若x-4=9,则x=8-4 | B. | 若2(2x+3)=2,则4x+6=2 | ||
| C. | 若-$\frac{1}{2}$x=4,则x=-2 | D. | 若$\frac{1}{3}$-$\frac{x-1}{2}$=1,则去分母得2-3(x-1)=1 |
8. 如图,在△ABC中,AB=AC=13,BC=24,D是线段BC上的动点(不含端点B,C),若线段AD长为正整数,则点D的个数共有( )
如图,在△ABC中,AB=AC=13,BC=24,D是线段BC上的动点(不含端点B,C),若线段AD长为正整数,则点D的个数共有( )
 如图,在△ABC中,AB=AC=13,BC=24,D是线段BC上的动点(不含端点B,C),若线段AD长为正整数,则点D的个数共有( )
如图,在△ABC中,AB=AC=13,BC=24,D是线段BC上的动点(不含端点B,C),若线段AD长为正整数,则点D的个数共有( )| A. | 15个 | B. | 14个 | C. | 13个 | D. | 12个 |
13.今有甲、乙、丙三名候选人参与某村村长选举,共发出1800张选票,得票数最高者为当选人,且废票不计入任何一位候选人之得票数内,全村设有四个投开票所,目前第一、第二、第三投开票所已开完所有选票,剩下第四投开票所尚未开票,结果如表所示:
(单位:票)
请回答下列问题:
(1)请分别写出目前甲、乙、丙三名候选人的得票数;
(2)承(1),请分别判断甲、乙两名候选人是否还有机会当选村长,并详细解释或完整写出你的解题过程.
| 投开票所 | 候选人 | 废票 | 合计 | ||
| 甲 | 乙 | 丙 | |||
| 一 | 200 | 211 | 147 | 12 | 570 |
| 二 | 286 | 85 | 244 | 15 | 630 |
| 三 | 97 | 41 | 205 | 7 | 350 |
| 四 | 250 | ||||
请回答下列问题:
(1)请分别写出目前甲、乙、丙三名候选人的得票数;
(2)承(1),请分别判断甲、乙两名候选人是否还有机会当选村长,并详细解释或完整写出你的解题过程.
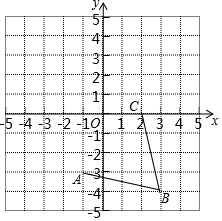 如图,在平面直角坐标系中,网格中每一个小正方形的边长为1个单位长度,且点A、B、C均在格点上.
如图,在平面直角坐标系中,网格中每一个小正方形的边长为1个单位长度,且点A、B、C均在格点上.