题目内容
14.若方程$\frac{3-2x}{x-3}$+$\frac{mx+2}{3-x}$=-1无解,则m的值是-3或-$\frac{5}{3}$.分析 根据分式方程的解法即可求出答案.
解答 解:去分母得:3-2x-(mx+2)=x-3
∴3-2x-mx-2=x-3
∴(m+3)x=4
当m+3=0时,
此时方程无解,符合题意,
此时m=-3,
当m+3≠0时,
由于方程无解,
将x=$\frac{4}{m+3}$代入x-3,得x-3=0,
∴解得:m=-$\frac{5}{3}$
故答案为:-3或-$\frac{5}{3}$
点评 本题考查分式方程的解法,解题的关键是熟练运用分式方程的解法,本题属于中等题型.

练习册系列答案
相关题目
4. 如图中物体的左视图是( )
如图中物体的左视图是( )
 如图中物体的左视图是( )
如图中物体的左视图是( )| A. |  | B. |  | C. |  | D. |  |
2.若$\sqrt{x+3}$+(y-2)2=0,则(x+y)2017等于( )
| A. | -1 | B. | 1 | C. | 52017 | D. | -52017 |
9.在下列式子$\frac{x}{2}$,-3a,$\frac{x}{y}$,$\frac{2s+t}{π}$,$\frac{3}{5+x}$,a2+2ab+$\frac{2}{3}$b2中,分式的个数有( )
| A. | 0个 | B. | 1个 | C. | 2个 | D. | 3个 |
19.下列方程的变形中,正确的是( )
| A. | 若x-4=9,则x=8-4 | B. | 若2(2x+3)=2,则4x+6=2 | ||
| C. | 若-$\frac{1}{2}$x=4,则x=-2 | D. | 若$\frac{1}{3}$-$\frac{x-1}{2}$=1,则去分母得2-3(x-1)=1 |
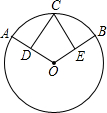 如图,在⊙O中,$\widehat{AC}$=$\widehat{CB}$,CD⊥OA于D,CE⊥OB于E,求证:AD=BE.
如图,在⊙O中,$\widehat{AC}$=$\widehat{CB}$,CD⊥OA于D,CE⊥OB于E,求证:AD=BE.