题目内容
16.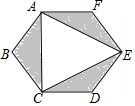 如图,正六边形ABCDEF是一块绿化带,阴影部分都是花圃,一只自由飞翔的小鸟,将随机落在这块绿化带上,则小鸟在花圃上的概率为$\frac{1}{2}$.
如图,正六边形ABCDEF是一块绿化带,阴影部分都是花圃,一只自由飞翔的小鸟,将随机落在这块绿化带上,则小鸟在花圃上的概率为$\frac{1}{2}$.
分析 根据正六边形的特点求出阴影部分的面积和空白部分的面积,再根据概率公式即可得出答案.
解答 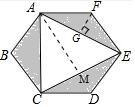 解:设正六边形的边长a,则FG=$\frac{a}{2}$,
解:设正六边形的边长a,则FG=$\frac{a}{2}$,
∵AG=$\sqrt{A{F}^{2}-F{G}^{2}}$=$\frac{\sqrt{3}}{2}$a,
∴AE=$\sqrt{3}$a,
∴阴影部分的面积是:$\frac{1}{2}$AE•FG×3=$\frac{1}{2}$×$\sqrt{3}$a×$\frac{1}{2}$a×3=$\frac{3}{4}$$\sqrt{3}$a2,
空白部分的面积是:$\frac{1}{2}$CE•AM=$\frac{1}{2}$×$\sqrt{3}$a×$\frac{3}{2}$a=$\frac{3}{4}$$\sqrt{3}$a2,
∴小鸟在花圃上的概率为$\frac{1}{2}$;
故答案为:$\frac{1}{2}$.
点评 此题主要考查了几何概率问题,用到的知识点为:概率=相应的面积与总面积之比.

练习册系列答案
相关题目
7.已知|a+b-1|+$\sqrt{2a+b-2}$=0,则(a-b)2017的值为( )
| A. | 1 | B. | -1 | C. | 2015 | D. | -2015 |
4. 如图中物体的左视图是( )
如图中物体的左视图是( )
 如图中物体的左视图是( )
如图中物体的左视图是( )| A. |  | B. |  | C. |  | D. |  |
11.2016年某县投入500万元用于该县的精准扶贫,预计到2018年该项投入将达720万元,若该项投入每年的增长率都为x,则下列方程正确的是( )
| A. | 500(1+x)=720 | B. | 500(1+x)2=720 | ||
| C. | 500(1+x)+500(1+x)2=720 | D. | 500x2=720 |
1.下列是一元二次方程的为( )
| A. | x2-4y+5=0 | B. | x2=0 | C. | ax2+bx+c=0 | D. | x2-$\frac{1}{x}$=2 |