题目内容
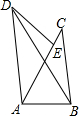 如图所示,在△ABC中,∠BAC=45°,将△ABC绕点A逆时针旋转后,能与△AED重合,已知AB=3,AC=4,则BD的长度为( )
如图所示,在△ABC中,∠BAC=45°,将△ABC绕点A逆时针旋转后,能与△AED重合,已知AB=3,AC=4,则BD的长度为( )| A、5 | B、4 | C、3 | D、6 |
考点:旋转的性质
专题:
分析:如图,证明AC=AD=4,∠DAE=∠CAB=45°,得到∠DAB=90°;由勾股定理即可解决问题.
解答: 解:由题意得:△ABC≌△AED,
解:由题意得:△ABC≌△AED,
∴AC=AD=4,∠DAE=∠CAB=45°,
∴∠DAB=90°;由勾股定理得:
BD2=AB2+AD2,∵AB=3,∴BD=5,
故选A.
 解:由题意得:△ABC≌△AED,
解:由题意得:△ABC≌△AED,∴AC=AD=4,∠DAE=∠CAB=45°,
∴∠DAB=90°;由勾股定理得:
BD2=AB2+AD2,∵AB=3,∴BD=5,
故选A.
点评:该题主要考查了旋转变换的性质、勾股定理等几何知识点及其应用问题;应牢固掌握旋转变换的性质、勾股定理等几何知识点.

练习册系列答案
 中考利剑中考试卷汇编系列答案
中考利剑中考试卷汇编系列答案
相关题目
已知B是线段AC上的一点,且BC=
AB,D是AC的中点,若DC=2cm,则AB的长为( )
| 1 |
| 3 |
| A、4cm | ||
| B、3cm | ||
| C、2cm | ||
D、
|
菱形的周长为100cm,一条对角线长为14cm,它的面积是( )
| A、168cm2 |
| B、336cm2 |
| C、672cm2 |
| D、84cm2 |
观察下列多项式,是完全平方式的是( )
| A、x2-4x+2 |
| B、x2+x+1 |
| C、x2-4x-4 |
| D、4x2+4x+1 |
 如图,四边形ABCD中,AB=AD,AD∥BC,∠ABC=60°,∠BCD=30°,若BC=6,试求△ACD的面积.
如图,四边形ABCD中,AB=AD,AD∥BC,∠ABC=60°,∠BCD=30°,若BC=6,试求△ACD的面积.