题目内容
在△ABC中,AB=AC,AD是中线,△ABC的周长为34cm,△ABD的周长为30cm,则AD的长为 cm.
考点:等腰三角形的性质
专题:
分析:先求出AB+BD=
(AB+AC+BC)=17,即可求出AD=(AB+BD+AD)-(AB+BD)=30-17=13cm.
| 1 |
| 2 |
解答:解:∵AB=AC,D是中点,
且AB+AC+BC=34,
∴BD=
BC,AB=
(AB+AC),
∴AB+BD=
(AB+AC)+
BC=
(AB+AC+BC)=17cm,
∵AB+BD+AD=30cm,
∴AD=30-17=13(cm);
故答案为13.
且AB+AC+BC=34,
∴BD=
| 1 |
| 2 |
| 1 |
| 2 |
∴AB+BD=
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
∵AB+BD+AD=30cm,
∴AD=30-17=13(cm);
故答案为13.
点评:本题考查了等腰三角形的性质和三角形的中线;弄清各条线段之间的关键是解题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
如果x2+ax+1是一个完全平方式,那么a的值是( )
| A、2 | B、-2 | C、±2 | D、±1 |
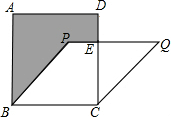 如图所示,正方形ABCD与菱形PQCD的面积分别为25cm2和20cm2,阴影部分的面积为
如图所示,正方形ABCD与菱形PQCD的面积分别为25cm2和20cm2,阴影部分的面积为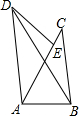 如图所示,在△ABC中,∠BAC=45°,将△ABC绕点A逆时针旋转后,能与△AED重合,已知AB=3,AC=4,则BD的长度为( )
如图所示,在△ABC中,∠BAC=45°,将△ABC绕点A逆时针旋转后,能与△AED重合,已知AB=3,AC=4,则BD的长度为( ) 如图,已知A(-4,a),B(-1,2)是一次函数y1=kx+b与反比例函数y2=
如图,已知A(-4,a),B(-1,2)是一次函数y1=kx+b与反比例函数y2=