题目内容
13.计算.(1)$3\sqrt{3}-\sqrt{8}+\sqrt{2}-\sqrt{27}$
(2)$({2\sqrt{5}+5\sqrt{2}})({2\sqrt{5}-5\sqrt{2}})-{({\sqrt{5}-\sqrt{2}})^2}$
(3)$\sqrt{\frac{3}{2}}-({\frac{5}{2}\sqrt{\frac{3}{2}}+3\sqrt{\frac{1}{6}}-\sqrt{6}})$.
分析 (1)先把各二次根式化为最简二次根式,然后合并即可;
(2)利用平方差公式和完全平方公式计算;
(3)先把各二次根式化为最简二次根式,然后去括号后合并即可.
解答 解:(1)原式=3$\sqrt{3}$-2$\sqrt{2}$+$\sqrt{2}$-3$\sqrt{3}$
=-$\sqrt{2}$;
(2)原式=20-50-(5-2$\sqrt{10}$+2)
=-30-7+2$\sqrt{10}$
=-37+2$\sqrt{10}$;
(3)原式=$\frac{\sqrt{6}}{2}$-$\frac{5\sqrt{6}}{4}$-$\frac{\sqrt{6}}{2}$+$\sqrt{6}$
=-$\frac{\sqrt{6}}{4}$.
点评 本题考查了二次根式的计算:先把各二次根式化为最简二次根式,再进行二次根式的乘除运算,然后合并同类二次根式.在二次根式的混合运算中,如能结合题目特点,灵活运用二次根式的性质,选择恰当的解题途径,往往能事半功倍.

练习册系列答案
 名师点睛字词句段篇系列答案
名师点睛字词句段篇系列答案
相关题目
8.李老师对某班学生“你最喜欢的体育项目是什么?”的问题进行了调查,每位同学都选择了其中的一项,现把所得的数据绘制成频数分布直方图(如图).如图中的信息可知,该班学生最喜欢足球的频率是( )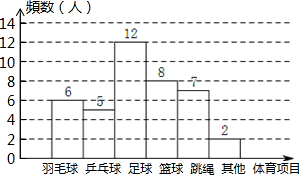

| A. | 12 | B. | 0.3 | C. | 0.4 | D. | 40 |
8.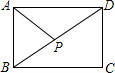 如图,在矩形ABCD中,连接BD,动点P从点B出发,依次沿BD→DC→CB运动至点B停止,设点P的运动路程为x,△APB的面积为y,则下列图象能大致刻画x与y之间的函数关系的是( )
如图,在矩形ABCD中,连接BD,动点P从点B出发,依次沿BD→DC→CB运动至点B停止,设点P的运动路程为x,△APB的面积为y,则下列图象能大致刻画x与y之间的函数关系的是( )
 如图,在矩形ABCD中,连接BD,动点P从点B出发,依次沿BD→DC→CB运动至点B停止,设点P的运动路程为x,△APB的面积为y,则下列图象能大致刻画x与y之间的函数关系的是( )
如图,在矩形ABCD中,连接BD,动点P从点B出发,依次沿BD→DC→CB运动至点B停止,设点P的运动路程为x,△APB的面积为y,则下列图象能大致刻画x与y之间的函数关系的是( )| A. |  | B. | 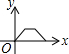 | C. | 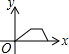 | D. | 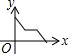 |
2.对于任意的正数m、n定义运算※为:m?n=$\left\{\begin{array}{l}{\sqrt{m}-\sqrt{n}(m≥n)}\\{\sqrt{m}+\sqrt{n}(m<n)}\end{array}\right.$,计算(3?2)+(8?12)的结果为( )
| A. | $\sqrt{3}$+$\sqrt{2}$ | B. | 2$\sqrt{3}$ | C. | $\sqrt{2}$+3$\sqrt{3}$ | D. | $\sqrt{3}$-$\sqrt{2}$ |